Video giảng Toán 7 Kết nối luyện tập chung trang 58

Tóm lược nội dung

CHƯƠNG III. GÓC VÀ ĐƯỜNG THẲNG SONG SONG

LUYỆN TẬP CHUNG TRANG 58

Xin chào các em học sinh thân mến, chúng ta lại gặp nhau trong bài học ngày hôm nay rồi!

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Cách viết giả thiết, kết luận và trình bày chứng minh định lí bằng kí hiệu.
• HS bước đầu biết suy luận để chứng minh một định lí.

HOẠT ĐỘNG KHỞI ĐỘNG

Trước khi bước vào bài học ngày hôm nay, các em suy nghĩ và trả lời câu hỏi: Em hãy nêu tính chất của hai đường thẳng song song?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

Nội dung 1: Phân tích Ví dụ

Em hãy:

+ Nêu giả thiết, kết luận của định lí?

+ để chứng minh uOv là góc vuông thì ta có thể chỉ ra tổng hai góc uOy và yOv bằng bao nhiêu độ?

+ Sử dụng tính chất về tia phân giác của một góc hãy chỉ ra mối quan hệ giữ góc  với , tương tự với , rồi so sánh tổng.

HOẠT ĐỘNG LUYỆN TẬP

Để củng cố lại kiến thức, bây giờ chúng ta cùng hoàn thành nhanh các bài tập sau đây:

Câu 1: Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Câu 2: Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng:

a) a // b;

b) c // d;

c) b ⊥ d.

Video trình bày nội dung:

Câu 1:

GT	a khác b,
KL	a // b.

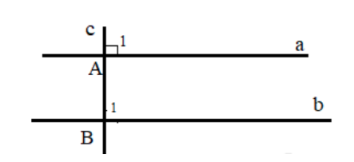
Câu 2:

a) : Cát tuyến  cắt hai đường thẳng phân biệt  và  tạo thành hai góc đồng vị bằng nhau (vì cùng là góc vuông) nên  

b) : Cát tuyến  cắt hai đường thẳng phân biệt  và  tạo thành hai góc đồng vị bằng nhau (vì cùng là góc vuông) nên  

c) : đường thẳng  cắt hai đường thẳng song song  và  thì tạo nên hai góc đổng vị bằng nhau, một góc là góc vuông (do  vuông góc với  ) nên góc giữa  và  cũng là góc vuông.

………..

Nội dung video Luyện tập chung còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.