Giải Câu 63 Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

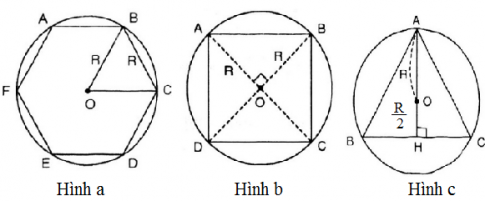
a) Hình a.

Gọi \({a_i}\)  là cạnh của đa giác đều i cạnh.

\({a_6}= R\) (vì \(O{A_1}{A_2}\) là tam giác đều)

Cách vẽ: vẽ đường tròn \((O;R)\). Trên đường tròn ta đặt liên tiếp các cung \(\overparen{{A_1}{A_2}}\),  \(\overparen{{A_2}{A_3}}\),...,\(\overparen{{A_6}{A_1}}\) mà căng cung có độ dài bằng \(R\). Nối \({A_1}\) với \({A_2}\), \({A_2}\) với \({A_3}\),…, \({A_6}\) với \({A_1}\) ta được hình lục giác đều \({A_1}\)\({A_2}\)\({A_3}\)\({A_4}\)\({A_5}\)\({A_6}\) nội tiếp đường tròn

b) Hình b

Cách vẽ như bài 61.

Trong tam giác vuông \(O{A_1}{A_2}\): \({a^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow a = R\sqrt 2 \)

c) Hình c

\({A_1}H\) =\( R\) +\(\frac{R}{2}\) =  \(\frac{3R}{2}\)

\({A_3}H\) = \(\frac{a}{2}\)

\({A_1}\)\({A_3}\)= \(a\)

Trong tam giác vuông \({A_1}H{A_3}\) ta có: \({A_1}{H^2} = {A_1}{A_3}^2 - {A_3}{H^2}\).

Từ đó \(\frac{9R^{2}}{4}\) = \(a^2\) - \(\frac{a^{2}}{4}\).

\(\Rightarrow{a^2} = 3{R^2} \Rightarrow a = R\sqrt 3 \)

Cách vẽ như câu a) hình a.

Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác \({A_1}{A_3}{A_5}\)  như trên hình c