Giải bài 6.22 bài phương trình quy về phương trình bậc hai

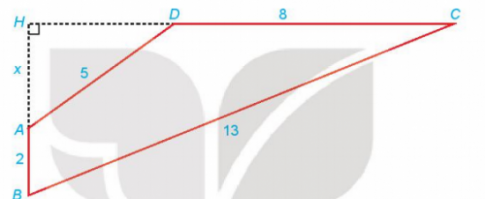
• Xét tam giác AHD vuông tại H có: HD = $\sqrt{25-x^{2}}$ (áp dụng định lí Pytago).
• Xét tam giác BHC vuông tại H có: $HB^{2}+HC^{2}=BC^{2}$

=> $(x+2)^{2}+\left ( \sqrt{25-x^{2}} +8\right )^{2}=13^{2}$

$\Leftrightarrow 4\sqrt{25-x^{2}}=19-x$

Bình phương hai vế ta được:

$16.(25-x^{2}) =361 - 38x +x^{2}$

$\Leftrightarrow 17x^{2}-38x-39=0$

$\Leftrightarrow$ $x= 3$ hoặc $x= \frac{-13}{17}$

Thử lại phương trình và điều kiện x > 0, giá trị $x= 3$ thỏa mãn.

Vậy AH = x = 3.

• Diện tích tam giác HAD là: $S_{HAD}=\frac{1}{2}AH.HD=6$
• Diện tích tam giác HBC là: $S_{HAD}=\frac{1}{2}HB.HC=36$

Vậy diện tích tứ giác ABCD là: 36 - 6 = 30 (đơn vị diện tích).