Cho tam giác ABC có góc A bằng $120^{\circ}$.
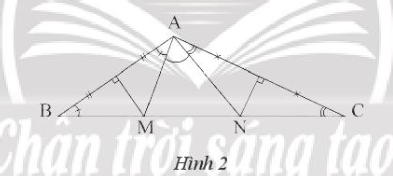
Bài 3. Cho tam giác ABC có góc A bằng $120^{\circ}$. Các đường trung trực của AB và AC lần lượt cắt BC tại M và N. Tính số đo góc MAN.
Ta có MA = MB, suy ra tam giác MAB cân tại M suy ra $\widehat{MAB}=\widehat{MBA}=\widehat{B}$
Tương tự, ta có tam giác NAC cân tại N, suy ra $\widehat{NAC}=\widehat{NCA}=\widehat{C}$
Ta có: $\widehat{MAN}=\widehat{BAC}-(\widehat{MAB}+\widehat{NAC})$
$=120^{\circ}-(\widehat{B}+\widehat{C}=120^{\circ}-60^{\circ}=60^{\circ}$

Bình luận