Cho góc xOy. Lấy hia điểm A, B thuộc tia Ox sao cho OA < OB.
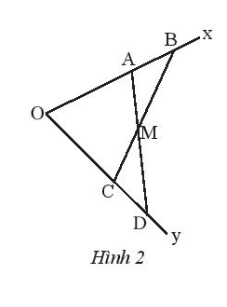
Bài 9. Cho góc xOy. Lấy hia điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OA = OC, OB = OD. Gọi M là giao điểm của AD và CB. Chứng minh rằng:
a) AD = CB;
b) $\Delta MAB = \Delta MCD$
a) Ta có $\Delta AOD=\Delta COB$ (c.g.c), suy ra AD = CB.
b) Ta có $\Delta AOD =\Delta COB$ (chứng minh trên)
Do đó $\widehat{MBA}=\widehat{MDC};\widehat{MAB}=\widehat{MCD}$ (cùng bù hai góc bằng nhau)
Ta lại có OA =OC, OB = OD, do đó AB = CD.
Suy ra $\Delta MAB= \Delta MCD$ (g.c.g)
Xem toàn bộ: Giải SBT toán 7 Chân trời bài 2 Tam giác bằng nhau
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận