Cho góc xOy bằng $45^{\circ}$ và điểm M nằm trong góc xOy.
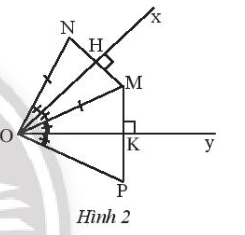
Bài 2. Cho góc xOy bằng $45^{\circ}$ và điểm M nằm trong góc xOy. Vẽ điểm N sao cho Ox là trung trực của MN, vẽ điểm P sao cho Oy là trung trực của MP.
a) Chứng minh ON = OP.
b) Tính số đo góc NOP.
a) Ta có Ox là trung trực MN, suy ra OM = ON.
Ta có Oy là trung trực của MP, suy ra OM = OP. Vậy ON = OP.
b) Gọi H và K lần lượt là trung điểm của MN và MP.
Ta có $\Delta OHM =\Delta OHN; \Delta OKM=\Delta OKP$ (c.c.c)
Suy ra $\widehat{NOP}=\widehat{NOM}+\widehat{MOP}$=$2(\widehat{xOM}+\widehat{MOy})=2\widehat{xOy}=2\times 45^{\circ}=90^{\circ}$

Bình luận