5.8 Một người lái xe chữa cháy nhận lệnh đến một vụ cháy đặc biệt quan trọng. Đường nhanh nhất có thể đến đám cháy phải qua một chiếc cầu có dạng cung tròn với bán kính cong R = 50,0 m

Một trong số những giải pháp dễ thực hiện đối với người lái xe đó là tăng tốc (từ dưới chân cầu) đến vận tốc cần thiết và điều khiển xe chuyển động tròn đều qua cầu với vận tốc v.

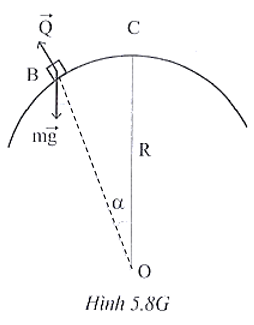
Khi xe chuyển động tròn đều trên cầu, theo định luật II Newton tại mọi vị trí ta luôn có: $m\vec{g}+\vec{Q}=m\vec{a}$

Chọn chiều dương (+) hướng vào tâm:

$mgcos\alpha -Q=m\frac{v^{2}}{R}\Rightarrow Q=mgcos\alpha -m\frac{v^{2}}{R}$

Theo định luật III Newton thì áp lực xe tác dụng lên cầu có độ lớn là:

$N=Q=mgcos\alpha -m\frac{v^{2}}{R}$

Vậy N lớn nhất khi $\alpha $ = 0 và giá trị đó không được vượt giới hạn áp lực cho phép của cầu.

Ta có: $P-m\frac{v^{2}}{R}\leq N_{max}$

$\Rightarrow v\geq \sqrt{\frac{P-N_{max}}{m}.R}=\sqrt{\frac{200000-60000}{20000}.50}\approx 18,7 m/s\approx 67,3km/h$