Giải bài 3 trang 69 toán 9 tập 2 ctst
Giải chi tiết bài 3 trang 69 sgk toán 9 tập 2 ctst
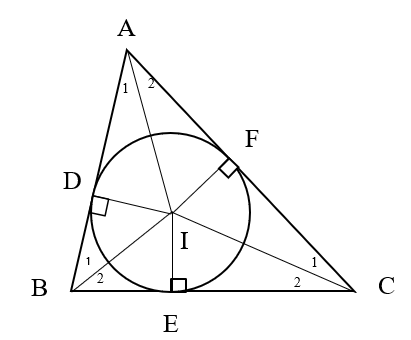
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).
a) Chứng minh 2AD = AB + AC – BC.
b) Tìm các hệ thức tương tự như ở câu a.
a) - Vì I là tâm đường tròn nội tiếp ![]() ABC
ABC
![]() I là giao điểm của ba đường phân giác
I là giao điểm của ba đường phân giác ![]() ABC
ABC
![]() .
.
- Xét ![]() ADI và
ADI và ![]() AFI có:
AFI có:
ID = IF = R;
![]() (chứng minh trên);
(chứng minh trên);
AI chung.
![]()
![]() ADI =
ADI = ![]() AFI (c – g – c).
AFI (c – g – c).
![]() AD = AF (hai cạnh tương ứng) (1).
AD = AF (hai cạnh tương ứng) (1).
- Chứng minh tương tự, ta được:
![]() DBI =
DBI = ![]() EIB (c – g – c)
EIB (c – g – c) ![]() BD = BE (hai cạnh tương ứng) (2).
BD = BE (hai cạnh tương ứng) (2).
![]() FCI =
FCI = ![]() ECI (c – g – c)
ECI (c – g – c) ![]() FC = EC (hai cạnh tương ứng) (3).
FC = EC (hai cạnh tương ứng) (3).
- Ta có: AB + AC – BC = AD + BD + AF + FC – BE – EC (4).
Thay (1), (2), (3) vào (4) ta được:
AB + AC – BC = AD + BE + AD + EC – BE – EC = 2AD (điều phải chứng minh).
b) Các hệ thức tương tự như ở câu a:
- 2AF = AB + AC – BC;
- 2BD = 2BE = AB + BC – AC;
- 2EC = 2FC = AC + BC – AB.
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận