Giải câu 27 bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông sgk Toán Hình 9 tập 1 Trang 88

a.   

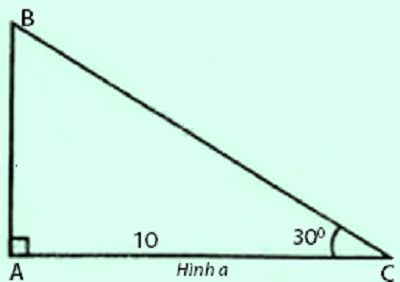
Ta có :  $\widehat{B}=90^{\circ}-30^{\circ}=60^{\circ}$

Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có :

$AB=AC.\tan C=10.\tan 30^{\circ}\approx 5,774(cm)$

$BC=\frac{AC}{\cos C}=\frac{10}{\cos 30^{\circ}}\approx 11,547$

Vậy tam giác vuông ABC có $\left\{\begin{matrix}AC=10 cm &  & \\ AB\approx 5,774 cm &  & \\ BC\approx 11,547 cm &  &\end{matrix}\right.$ và $\left\{\begin{matrix}\widehat{A}=90^{\circ} &  & \\ \widehat{C}=30^{\circ} &  & \\ \widehat{B}=60^{\circ} &  & \end{matrix}\right.$

b.

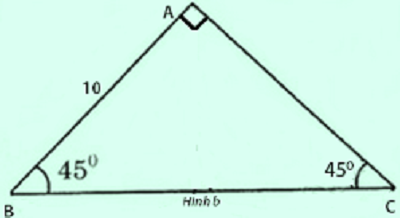
Ta có :  $\widehat{B}=90^{\circ}-45^{\circ}=45^{\circ}$

=> AC = AB = 10cm   ( vì ABC là tam giác vuông cân  )

Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có :

$BC=\frac{AB}{\sin C}=\frac{10}{\sin 45^{\circ}}\approx 14,142(cm)$

Vậy tam giác vuông ABC có $\left\{\begin{matrix}AC=10 cm &  & \\ AB=10cm &  & \\ BC\approx 14,142 cm &  &\end{matrix}\right.$ và $\left\{\begin{matrix}\widehat{A}=90^{\circ} &  & \\ \widehat{C}=40^{\circ} &  & \\ \widehat{B}=40^{\circ} &  & \end{matrix}\right.$

c.

Ta có  :  $\widehat{C}=90^{\circ}-35^{\circ}=55^{\circ}$

Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có :

$AB=BC.\cos B=20.\cos 35\approx 16,383$

$AC=BC.\sin B=20.\sin 35\approx 11,472$

Vậy tam giác vuông ABC có  $\left\{\begin{matrix}BC=20 cm &  & \\ AC\approx 11,472 cm &  & \\ AB\approx 16,383 cm & &\end{matrix}\right.$ và $\left\{\begin{matrix}\widehat{A}=90^{\circ} &  & \\ \widehat{C}=55^{\circ} &  & \\ \widehat{B}=35^{\circ} &  & \end{matrix}\right.$

d. 

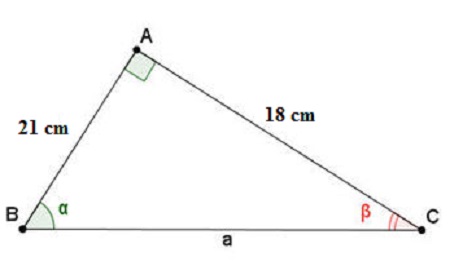
Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ABC , ta có :

$\tan B=\frac{AC}{AB}=\frac{18}{21}\approx 0,8571$

=>  $\widehat{B}\approx 41^{\circ}$

=>  $\widehat{C}=90^{\circ}-41^{\circ}=49^{\circ}$

ÁP dụng định lí Py-ta-go , ta có : $BC^{2}=AB^{2}+AC^{2}$

=> $BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{21^{2}+18^{2}}\approx 27,659(cm)$

Vậy tam giác vuông ABC có  $\left\{\begin{matrix}AC=18 cm &  & \\ AB=21 cm &  & \\ BC\approx 27,659 cm & &\end{matrix}\right.$ và $\left\{\begin{matrix}\widehat{A}=90^{\circ} &  & \\ \widehat{C}=49^{\circ} &  & \\ \widehat{B}=41^{\circ} &  & \end{matrix}\right.$