Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: f(x) > 0; f(x) < 0; f(x) ≥ 0 và f(x) ≤ 0

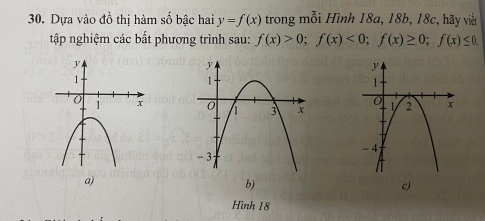
Xét hình 18a: dựa vào đồ thị y = f(x) ta có:

- Bất phương trình f(x) > 0 và f(x) ≥ 0 có tập nghiệm là rỗng (vô nghiệm).

- Bất phương trình f(x) <0  và f(x) ≤ 0 có tập nghiệm là R.

Xét hình 18b: dựa vào đồ thị y = f(x) ta có:

Với x ∈ (1; 3) hàm số nằm trên trục hoành ( f(x) > 0 ).

Với x < 1 hoặc x > 3 đồ thị hàm số nằm phía dưới trục hoành ( f(x) < 0 ).

Đồ thị hàm số cắt trục hoành tại x = 1 hoặc x = 3.

Vậy :

- f(x) > 0 khi x ∈ (1; 3).

- f(x) < 0 khi x ∈ (– ∞; 1) ∪ (3; +∞).

- f(x) ≥ 0 khi x ∈ [1; 3].

- f(x) ≤ 0 khi x ∈ (– ∞; 1] ∪ [3; +∞).

Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là (1; 3); (– ∞; 1) ∪ (3; +∞); [1; 3]; (– ∞; 1] ∪ [3; +∞).

Xét hình 18c: dựa vào đồ thị y = f(x), ta có :

Đồ thị hàm số cắt trục hoành tại x = 2 , x ≠ 2 hàm số nằm dưới trục hoành ( f(x) < 0 ).

Vậy :

- f(x) > 0 vô nghiệm.

- f(x) < 0 khi x ∈ ℝ \ {2}.

- f(x) ≥ 0 khi x = 2.

- f(x) ≤ 0 khi x ∈ ℝ.

Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là ∅; ℝ \ {2}; {2}; ℝ.