Giải bài 11 trang 82 toán 9 tập 2 ctst

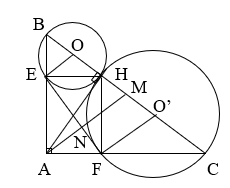
a) Ta có OO’ = OH + O’H = R + R’ và O; H; H’ thẳng hàng.

Hai đường tròn tiếp xúc nhau.

b) Xét đường tròn (O) có BH là đường kính

là góc nội tiếp chắn cung BH hay AB EH tại E.

Xét đường tròn (O’) có HC là đường kính

là góc nội tiếp chắn cung HC hay AC HF tại F.

Xét tứ giác AEHF có: 

          (chứng minh trên);

          (giả thiết);

          (chứng minh trên).

Tứ giác AEHF là hình chữ nhật.

c) Vì OE = OH = R nên OEH cân tại O .

Ta có ; .

Mà (chứng minh trên); (tính chất hình chữ nhật).

hay

EF OE tại E; E (O)

EF là đường trung tuyến đường tròn (O) (1).

Vì O’F = O’H = R’ O’HF cân tại O’

Mà (tính chất hình chữ nhật)

hay .

EF O’F tại F; F (O’)

EF là đường trung tuyến đường tròn (O’) (2).

Từ (1) và (2) điều phải chứng minh.

d) Ta có: (tổng ba góc trong của tam giác).

(tổng ba góc trong của tam giác).

mà (do AM = MC = BM = BC nên AMC cân tai M).

.

Xét ANF và EAF có: 

          chung

          (chứng minh trên).

ANF đồng dạng  EAF (g – g)

(EF = AH do AEHF là hình chữ nhật).

Xét AEF và ABC có: 

          chung

          (chứng minh trên).

AEF đồng dạng  ABC (g – g)

(EF = AH do AEHF là hình chữ nhật).

Ta có (hệ thức lượng trong tam giác vuông).

AH = 4,8 cm.

BC² = AB² + AC² = 6² + 8² =100 (Định lý Pytagore).

BC = 10 cm.

AH² = AF.AC (hệ thức lượng trong tam giác vuông).

= 2,88 cm.

Vậy = 5,53 cm².

= 1,99cm².