Câu hỏi tự luận mức độ vận dụng cao Toán 9 ctst bài 2: Xác suất của biến cố

Câu 1:

Gieo đồng thời hai con xúc xắc cân đối,  đồng chất I và II 

Ta có không gian mẫu: n(Ω) = 6. 6 = 36

*E: “Có đúng 1 con xúc xắc xuất hiện mặt 6 chấm”

- Xúc sắc I xuất hiện mặt 6 chấm,  xúc xắc II có thể xuất hiện 5 khả năng  suy ra  1. 5 = 5

- Xúc sắc II xuất hiện mặt 6 chấm,  xúc xắc I có thể xuất hiện 5 khả năng  suy ra  1. 5 = 5

suy ra  n(E) = 5+ 5 = 10

Do đó xác suất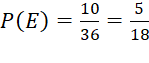

*F: "Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”

- Trường hợp có 1 xúc xắc xuất hiện mặt 6 chấm suy ra  1. 5+ 5. 1 = 10 khả năng

- Trường hợp 2,  cả hai xúc xắc đều là 6 chấm  suy ra  có 1. 1 khả năng 

suy ra  n(F) = 10+ 1 = 11

Do đó xác suất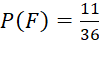  

* G:”Tích của hai số chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”

Những trường hợp tích hai số chấm xuất hiện trên con xúc xắc nhỏ hơn hoặc bằng 6 là: (1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 2); (2, 3); (3, 1); (3, 2); (4, 1); (5, 1)

Suy ra  n(G) = 12

Do đó xác suất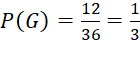

Câu 2: 

Bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1, 2, 3, 4, 5 , suy ra   n(Ω) = 2. 5 = 10

*E: “Rút được tấm thẻ ghi số lẻ”

- Đồng xu được gieo có thể xuất hiện mặt sấp hoặc lẻ,  tấm thẻ được rút có 3 kết quả có thể (1, 3, 5)

 suy ra n(E) = 2. 3 = 6

Do đó xác suất

* F: “Rút được tấm thẻ ghi số chẵn và đồng xu xuất hiện mặt sấp”

- Tấm thẻ được rút là số chẵn nên có 2 kết quả có thể xảy ra (2, 4);  đồng xu xuất hiện mặt sấp

 suy ra n(F) = 2. 1 = 2

Do đó xác suất

* G:”Rút được tấm thẻ ghi số 5 hoặc đồng xu xuất hiện mặt ngửa”

- Rút được tấm thẻ số 5  =>  có 1 khả năng xảy ra;  đồng xu có thể xuất hiện mặt sấp hoặc ngửa. 

- Đồng xu xuất hiện mặt ngửa  =>  có 1 khả năng;  tấm thẻ được rút có 5 khả năng có thể xảy ra. 

Suy ra n(G) = 1. 2+ 1. 5 = 7

Do đó xác suất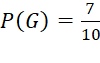

Câu 3: 

Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái  

Suy ra  n(Ω) = 4.2 = 8 phần tử

a) E: “Trong ba chữ cái,  có hai chữ H và một chữ T”

Rút từ túi I để được 2 chữ H  => 1 khả năng có thể 

Rút từ túi II để được chữ T  => 1 khả năng có thể

Suy ra   n(E) = 1.1 = 1

Do đó xác suất

b) F: “Trong ba chữ cái,  có nhiều nhất hai chữ T”

*Trường hợp có 1 chữ T

- Rút từ túi I,  có 2 khả năng có thể (TH, HT); rút từ túi II có 1 khả năng có thể xảy ra (H) , suy ra 2.1 = 2 khả năng 

- Rút từ túi I thẻ HH,  rút túi II thẻ T ,  suy ra 1.1 khả năng

Suy ra có 2 + 1 = 3 khả năng để trong ba chữ cái rút được một chữ T

*Trường hợp có 2 chữ T

- Rút túi I,  có 2 khả năng có thể (TH, HT); rút từ túi II có 1 khả năng có thể xảy ra (T),  suy ra 2.1 = 2 khả năng

- Rút từ túi I thẻ TT,  rút túi II thẻ H,  suy ra 1.1 khả năng

Suy ra   có 2 + 1 = 3 khả năng

Suy ra   n(F) = 3 + 3 = 6

Do đó xác suất