Lý thuyết trọng tâm toán 10 kết nối bài 27: Thực hành tính xác suất theo định nghĩa cổ điển
Tổng hợp kiến thức trọng tâm toán 10 kết nối tri thức bài 27 Thực hành tính xác suất theo định nghĩa cổ điển. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
CHƯƠNG VIII. ĐẠI SỐ TỔ HỢP
BÀI 27. THỰC HÀNH TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
1. SỬ DỤNG PHƯƠNG PHÁP TỔ HỢP
HĐ1:
Không thể được, vì số các tập con 6 phần tử của tập {1; 2;….; 45} là quá lớn.
Kết luận:
Trong nhiều bài toán, để tính số phần tử của không gian mẫu, của các biến cố, ta thường sử dụng các quy tắc đếm, các công thức tính số hoán vị, chỉnh hợp và tổ hợp.
Ví dụ 1 (SGK -tr83)
Luyện tập 1:
Không gian mẫu: n($\Omega $)=C$_{12}^{6}$ = 924.
Biến cố A: "6 học sinh được chọn số học sinh nữ bằng số học sinh nam".
Để số học sinh nữ bằng số học sinh nam thì chọn 3 nữ và 3 nam.
n(A) = C$_{7}^{3}$.C$_{5}^{3}$=350
Vậy P(A) = $\frac{350}{924}$=$\frac{25}{66}$
2. SỬ DỤNG SƠ ĐỒ HÌNH CÂY
HĐ2:
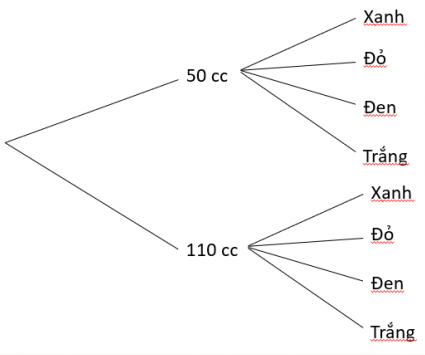
Nhìn vào sơ đồ hình cây ta thấy:
n($\Omega $)=8.
Kết luận:
Trong một số bài toán, phép thử T được hình thành từ một vài phép thử, chẳng hạn: gieo xúc xắc liên tiếp bốn lần; lấy ba viên bi, mỗi viên từ một hộp;… Khi đó ta sử dụng sơ đồ hình cây để có thể mô tả đầy đủ, trực quan không gian mẫu và biến cố cần tính xác suất.
Ví dụ 2 (SGK -tr84)
Luyện tập 2:
Theo như sơ đồ cây ở HĐ2 có n($\Omega $) = 8.
Biến cố A: "Người chơi nhận được loại xe 110 cc có màu trắng hoặc màu xanh"
Có n(A) = 2. Vậy P(A) = $\frac{2}{8}$=$\frac{1}{4}$.
Luyện tập 3:
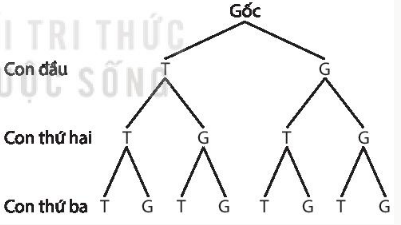
b) Vậy n(Ω) = 8.
Gọi biến cố A: " Gia đình đó có một con trai và hai con gái".
A = {GTG; TGG; GGT}
(với G là viết tắt của gái, T là viết tắt của trai).
n(A) = 3.
Vậy P(A) = $\frac{3}{8}$.
3. XÁC SUẤT CỦA BIẾN CỐ ĐỐI
HĐ3:
n($\bar{E}$)=n($\Omega $)-n(E).
Kết luận:
Cho E là một biến cố. Xác suất của biến cố $\bar{E}$ liên hệ với xác suất của E bởi công thức sau:
P($\bar{E}$)=1-P(E).
Ví dụ 3 (SGK -tr85)
Chú ý:
Trong một số bài toán, nếu tính trực tiếp xác suất của biến cố gặp khó khăn, ta có thể tính gián tiếp bằng cách tính xác suất của biến cố đối của nó.
Luyện tập 4:
a)
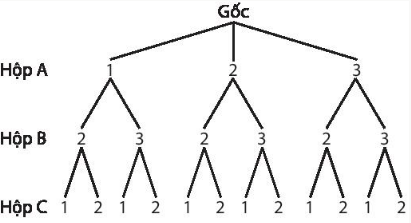
Từ sơ đồ hình cây ta có
$\Omega $={121;122;131;132;221;222;231;232;321;
322; 331; 332}. Vậy n($\Omega $)=12.
b) Biến cố đối $\bar{M}$ : "Trong ba thẻ rút ra không có thẻ số 1''.
Do đó $\bar{M}$={222;232;322;332}.n($\bar{M}$)=4.
c) P($\bar{M}$)=$\frac{4}{12}$=$\frac{1}{3}$.
Suy ra P(M)=1-$\frac{1}{3}$=$\frac{2}{3}$.
Vận dụng:
Ta có: n($\Omega $)=C$_{45}^{6}$
+ Biến cố F: "Bạn An trúng giải độc đắc".
F là tập hợp có duy nhất một phần tử là tập {5; 13; 20; 31; 32; 35}.
n(F) = 1.
Vậy P(F) = $\frac{1}{C_{45}^{6}}$=$\frac{1}{8145060}$.
+ Biến cố G: "Bạn An trúng giải nhất".
Mỗi phần tử của G được hình thành từ hai công đoạn.
Công đoạn 1: Chọn 5 phần tử trong tập {5; 13; 20; 31; 32; 35}, có C$_{6}^{5}$=6 (cách chọn).
Công đoạn 2: Chọn 1 phần tử còn lại trong 39 phần tử không thuộc tập {5; 13; 20; 31; 32; 35}, có C$_{39}^{1}$=39 (cách chọn).
Suy ra: n(G) = 6. 39 = 234 (phần tử).
Vậy P(G) = $\frac{234}{C_{45}^{6}}$=$\frac{39}{1357510}$.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận