Soạn giáo án điện tử Toán 12 CTST Bài tập cuối chương I

Nội dung giáo án

BÀI TẬP CUỐI CHƯƠNG I

CHÀO CẢ LỚP! CHÀO MỪNG CÁC EM TỚI BUỔI HỌC NÀY

KHỞI ĐỘNG

- GV tổ chức cho HS củng cố lại bài cũ trước khi bước vào nội dung chính của bài học mới.

HOẠT ĐỘNG LUYỆN TẬP 

HS quan sát các bài tập GV trình chiếu sau đây, tính toán và chọn ra đáp án đúng:

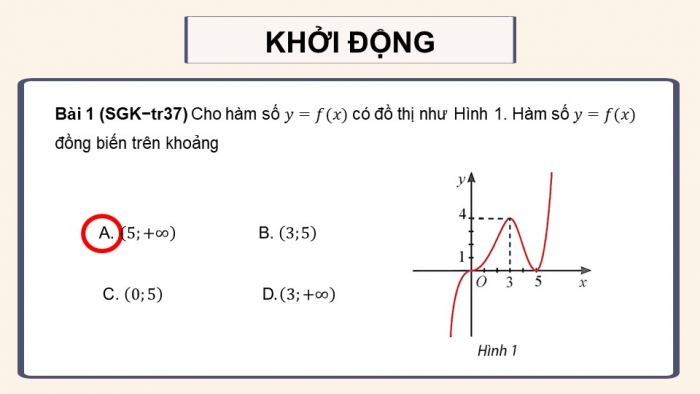
Câu 1 trang 37 toán 12 tập 1 ctst

Cho hàm số có đồ thị như Hình 1. Hàm số đồng biến trên khoảng: 

A.                                 B.

C.                                                D.

Bài giải: 

Đáp án A. (5; +∞)

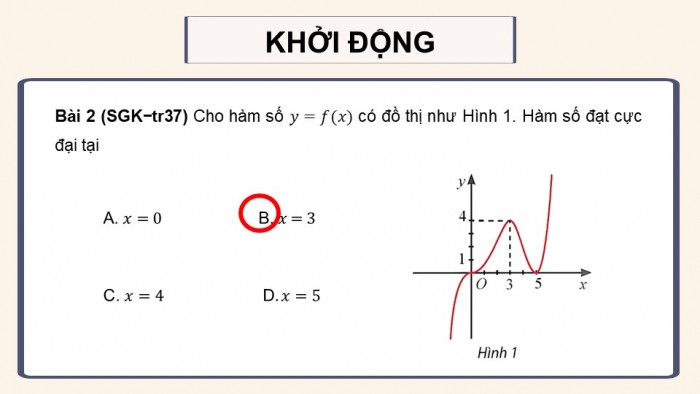
Câu 2 trang 37 toán 12 tập 1 ctst

Cho hàm số có đồ thị như Hình 1. Hàm số đạt cực đại tại

A.                                     B.

C.                                     D.

Bài giải: 

Đáp án B.

Câu 3 trang 37 toán 12 tập 1 ctst:

Cho hàm số Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đạt cực tiểu tại giá trị cực tiểu

B. Hàm số đạt cực tiểu tại giá trị cực tiểu

C. Hàm số đạt cực tiểu tại giá trị cực tiểu

D. Hàm số đạt cực tiểu tại giá trị cực tiểu

Bài giải: 

Đáp án B. Hàm số đạt cực tiểu tại giá trị cực tiểu

Tập xác định:

Ta có:

hoặc

Bảng biến thiên:

Vậy hàm số đạt cực tiểu tại giá trị cực tiểu

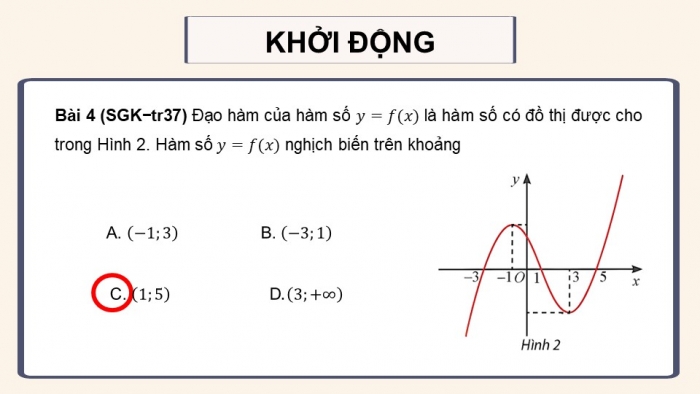
Câu 4 trang 37 toán 12 tập 1 ctst:

Đạo hàm của hàm số là hàm số có đồ thị được cho như Hình 2. Hàm số nghịch biến trên khoảng

A.                                  B.

C.                                     D.

Bài giải: 

Đáp án C.

Hàm số nghịch biến khi ; dựa vào đồ thị ta thấy trên đoạn , nên hàm số nghịch biến trên đoạn

Câu 5 trang 37 toán 12 tập 1 ctst:

Giá trị nhỏ nhất của hàm số: trên đoạn là

A.                                          B.

C.                                          D.

Bài giải: 

Đáp án C.

Tập xác định:

Ta có:

Vậy trên đoạn :

Câu 6 trang 37 toán 12 tập 1 ctst:

Tiệm cận xiên của đồ thị hàm số là đường thẳng có phương trình

A.                                                B.

C.                                                   D.

Bài giải: 

Đáp án A.

Tập xác định

Ta có:

Ta cũng có ;

Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng

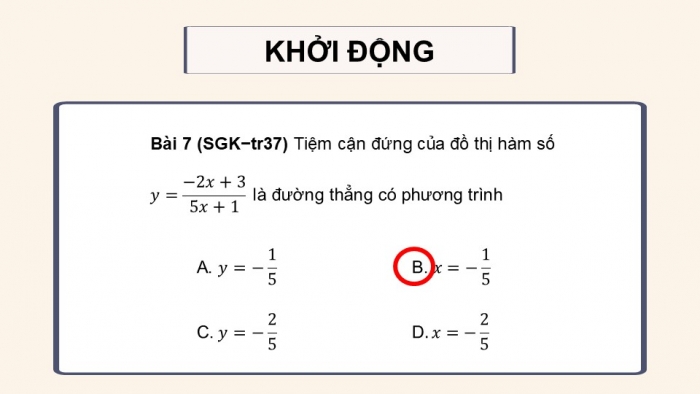
Câu 7 trang 37 toán 12 tập 1 ctst:

Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình

A.                                            B.

C.                                            D.

Bài giải: 

Đáp án B.

Tập xác định

Ta có ; . Suy ra đường thẳng là tiệm cận đứng của đồ thị hàm số

Câu 8 trang 38 toán 12 tập 1 ctst:

Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên và nghịch biến trên .

B. Hàm số đồng biến trên và .

C. Hàm số nghịch biến trên và .

D. Hàm số nghịch biến trên và .

Bài giải: 

Đáp án C. Hàm số nghịch biến trên và .

Tập xác định

Ta có . Vì nên hàm số nghịch biến trên mỗi khoảng và .

HOẠT ĐỘNG VẬN DỤNG

Bài 9 trang 38 toán 12 tập 1 ctst

Tìm hai số không âm và có tổng bằng 10 sao cho: 

a) Biểu thức đạt giá trị lớn nhất. 

b) Tổng bình phương của chúng đạt giá trị nhỏ nhất.

c) Biểu thức đạt giá trị lớn nhất.

Bài giải:

Tập xác định:

Đặt

a) Ta có:

Bảng biến thiên của hàm số trên đoạn

Từ bảng biến thiên, hàm số có giá trị lớn nhất tại , khi đó

b) Ta có:

Bảng biến thiên của hàm số trên đoạn

Từ bảng biến thiên, hàm số đạt giá trị nhỏ nhất tại , khi đó

c) Ta có:

; hoặc (loại)

Bảng biến thiên của hàm số trên đoạn

Từ bảng biến thiên, hàm số đạt giá trị lớn nhất tại ; khi đó

Bài 10 trang 38 toán 12 tập 1 ctst

Cho hàm số bậc ba có đồ thị như Hình 3. Viết công thức của hàm số.

Bài giải:

Phương trình tổng quát của hàm số:  

Đồ thị hàm số giao với tại điểm

Đồ thị hàm số đi qua điểm

Đạo hàm:  

Hàm số đạt cực trị tại hai điểm và ; do đó phương trình có hai nghiệm là hoặc . 

Ta có hệ phương trình:

Vậy công thức của hàm số 

HƯỚNG DẪN VỀ NHÀ

- HS củng cố lại kiến thức đã học.

- HS tìm tòi, mở rộng kiến thức, rèn luyện học tập.

- Xem trước nội dung bài 1 véc tơ và các phép toán trong không gian.

CHÚNG TA ĐÃ HOÀN THÀNH XUẤT SẮC BÀI HỌC, CHÀO TẠM BIỆT CÁC EM!