Bài giảng điện tử dạy thêm Toán 12 CD Bài tập cuối chương III
Tải giáo án điện tử dạy thêm Toán 12 Bài tập cuối chương III chương trình mới sách cánh diều. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu buổi chiều hoặc buổi 2. Giáo án có nhiều hình ảnh đẹp, tư liệu sinh động. Chắc chắn bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng. Powerpoint dạy thêm Toán 12 CD











Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC
HÔM NAY!
KHỞI ĐỘNG
Bảng sau thống kê lại số giờ nắng trong tháng 5 của các năm từ 2002 đến 2021 tại trạm quan trắc đặt ở một tỉnh.
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm trên.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
| Số giờ nắng | [130; 160) | [160; 190) | [190; 220) | [220; 250) | [250; 280) |
| Số năm | 2 | 1 | 6 | 7 | 4 |
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
b) Ta có bảng thống kê sau:
Giải:
| Nhóm | [130; 160) | [160; 190) | [190; 220) | [220; 250) | [250; 280) |
| Tần số | 2 | 1 | 6 | 7 | 4 |
| Tần số tích lũy | 2 | 3 | 9 | 16 | 20 |
Số phần tử của mẫu là
Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 3 là nhóm [190;220) có và nhóm 2 là nhóm [160;190) có .
Giải:
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 4 là nhóm [220;250) có và nhóm 3 là nhóm [190;220) có
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Khi đó,
c) Ta có bảng thống kê sau:
Giải:
| Nhóm | [130; 160) | [160; 190) | [190; 220) | [220; 250) | [250; 280) |
| Giá trị đại diện | 145 | 175 | 205 | 235 | 265 |
| Tần số | 2 | 1 | 6 | 7 | 4 |
Số trung bình cộng của mẫu số liệu ghép nhóm là:
Phương sai của mẫu số liệu ghép nhóm là:
Độ lệch chuẩn của mẫu số liệu ghép nhóm là .
CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO
MẪU SỐ LIỆU GHÉP NHÓM
BÀI TẬP CUỐI CHƯƠNG III
PHIẾU BÀI TẬP
Bài 1. Độ tuổi của các công nhân làm việc trong một công ty được thống kê trong bảng sau:
| Độ tuổi | [20;30) | [30; 40) | [40; 50) | [50; 60) |
| Số công nhân | 23 | 37 | 26 | 14 |
a) Tính khoảng biến thiên của số liệu mẫu ghép nhóm trên.
b) Tính khoảng tứ phân vị của số liệu mẫu ghép nhóm trên.
Giải:
a) Khoảng biến thiên của mẫu số liệu trên là: .
b) Ta có bảng thống kê sau:
| Nhóm | [20;30) | [30; 40) | [40; 50) | [50; 60) |
| Tần số | 23 | 37 | 26 | 14 |
| Tần số tích lũy | 23 | 60 | 86 | 100 |
Số phần tử của mẫu là .
Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 2 là nhóm [30; 40) có và nhóm 1 là nhóm [20; 30) có .
Giải:
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 3 là nhóm [40; 50) có và nhóm 2 là nhóm [30; 40) có .
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Khi đó,
Bài 2. Biểu đồ sau mô tả năng suất lúa của một thửa ruộng từ năm 2010 đến 2019 (đơn vị: tấn/ha):
Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Giải:
Ta có bảng thống kê sau:
| Nhóm | [5,5; 5,8) | [5,8; 6;1) | [6,1; 6;4) | [6,4; 6;7) | [6,7; 7) |
| Giá trị đại diện | 5,65 | 5,95 | 6,25 | 6,55 | 6,85 |
| Tần số | 1 | 1 | 3 | 4 | 1 |
Số trung bình cộng của mẫu số liệu ghép nhóm là:
Phương sai của mẫu số liệu ghép nhóm là:
Độ lệch chuẩn của mẫu số liệu ghép nhóm là .
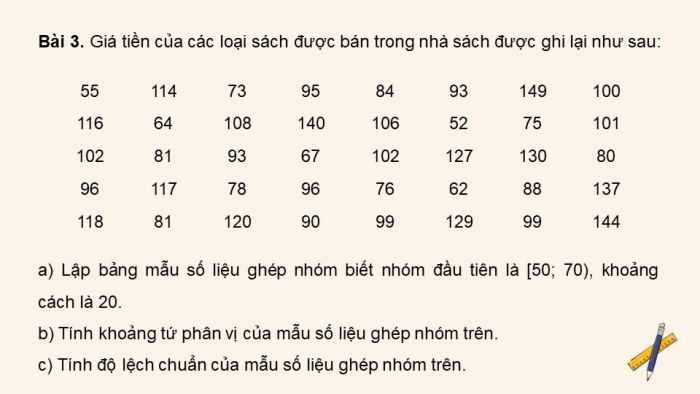
Bài 3. Giá tiền của các loại sách được bán trong nhà sách được ghi lại như sau:
| 55 | 114 | 73 | 95 | 84 | 93 | 149 | 100 |
| 116 | 64 | 108 | 140 | 106 | 52 | 75 | 101 |
| 102 | 81 | 93 | 67 | 102 | 127 | 130 | 80 |
| 96 | 117 | 78 | 96 | 76 | 62 | 88 | 137 |
| 118 | 81 | 120 | 90 | 99 | 129 | 99 | 144 |
a) Lập bảng mẫu số liệu ghép nhóm biết nhóm đầu tiên là [50; 70), khoảng cách là 20.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Giải:
a) Ta lập bảng mẫu số liệu ghép nhóm như sau:
| Giá tiền (nghìn đồng) | [50; 70) | [70; 90) | [90; 110) | [110; 130) | [130; 150) |
| Số sách | 5 | 9 | 14 | 7 | 5 |
b) Ta có bảng thống kê sau:
| Nhóm | [50; 70) | [70; 90) | [90; 110) | [110; 130) | [130; 150) |
| Tần số | 5 | 9 | 14 | 7 | 5 |
| Tần số tích lũy | 5 | 14 | 28 | 35 | 40 |
Số phần tử của mẫu là
Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 2 là nhóm [70; 90) có và nhóm 1 là nhóm [50; 70) có .
Giải:
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 4 là nhóm [110; 130) có và nhóm 3 là nhóm [90; 110) có
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Khi đó,
Giải:
c) Ta có bảng thống kê:
| Nhóm | [50; 70) | [70; 90) | [90; 110) | [110; 130) | [130; 150) |
| Tần số tích lũy | 60 | 80 | 100 | 120 | 140 |
| Tần số | 5 | 9 | 14 | 7 | 5 |
Số trung bình cộng của mẫu số liệu ghép nhóm là:
Phương sai của mẫu số liệu ghép nhóm là:
Độ lệch chuẩn của mẫu số liệu ghép nhóm là .
Bài 4. Tuổi thọ của một số linh kiện điện tử được sản xuất bởi hai phân xưởng được cho như sau:
| Tuổi thọ (năm) | [1; 2) | [2; 3) | [3; 4) | [4; 5) |
| Số linh kiện của phân xưởng 1 | 5 | 9 | 8 | 8 |
| Số linh kiện của phân xưởng 2 | 3 | 10 | 13 | 4 |
Tính khoảng tứ phân vị của mỗi mẫu số liệu trên và cho biết linh kiện của phân xưởng nào ít phân tán hơn.
Giải:
- Tính khoảng tứ phân vị của linh kiện của phân xưởng 1
| Nhóm | [1; 2) | [2; 3) | [3; 4) | [4; 5) |
| Tần số | 5 | 9 | 8 | 8 |
| Tần số tích lũy | 5 | 14 | 22 | 30 |
Số phần tử của mẫu là .
Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 2 là nhóm [2; 3) có và nhóm 1 là nhóm [1; 2) có .
Giải:
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng
Xét nhóm 3 là nhóm [3; 4) có và nhóm 2 là nhóm [2; 3) có
Áp dụng công thức, ta có tứ phân vị thứ ba là:
--------------- Còn tiếp ---------------
=> Xem toàn bộ Giáo án Powerpoint dạy thêm Toán 12 Cánh diều
Powerpoint dạy thêm Toán 12 CD, giáo án điện tử dạy thêm Bài tập cuối chương III Toán 12 cánh diều, giáo án PPT dạy thêm Toán 12 cánh diều Bài tập cuối chương III
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
