Bài giảng điện tử dạy thêm Toán 12 CD Bài 1: Khoảng biến thiên, khoáng tứ phân vị của mẫu số liệu ghép nhóm
Tải giáo án điện tử dạy thêm Toán 12 Bài 1: Khoảng biến thiên, khoáng tứ phân vị của mẫu số liệu ghép nhóm chương trình mới sách cánh diều. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu buổi chiều hoặc buổi 2. Giáo án có nhiều hình ảnh đẹp, tư liệu sinh động. Chắc chắn bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng. Powerpoint dạy thêm Toán 12 CD









Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
THÂN MẾN CHÀO ĐÓN CẢ LỚP
ĐẾN VỚI TIẾT HỌC HÔM NAY!
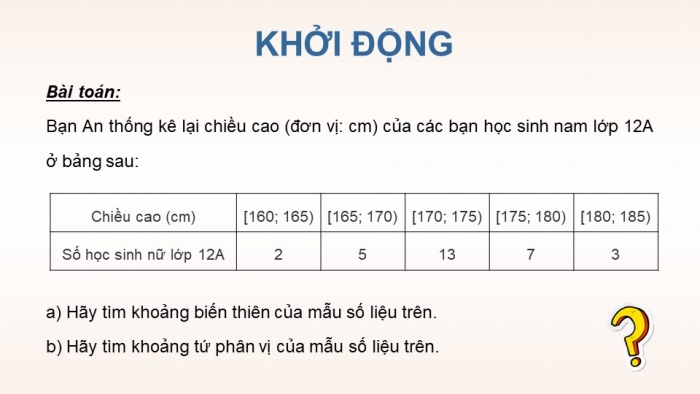
Bài toán:
Bạn An thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nam lớp 12A ở bảng sau:
KHỞI ĐỘNG
| Chiều cao (cm) | [160; 165) | [165; 170) | [170; 175) | [175; 180) | [180; 185) |
| Số học sinh nữ lớp 12A | 2 | 5 | 13 | 7 | 3 |
a) Hãy tìm khoảng biến thiên của mẫu số liệu trên.
b) Hãy tìm khoảng tứ phân vị của mẫu số liệu trên.
Giải:
a) Khoảng biên thiên của mẫu số liệu trên là:
b)
| Nhóm | [160; 165) | [165; 170) | [170; 175) | [175; 180) | [180; 185) |
| Tần số | 2 | 5 | 13 | 7 | 3 |
| Tần số tích lũy | 2 | 7 | 20 | 27 | 30 |
Số phần tử của mẫu là .
Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng .
Xét nhóm 3 là nhóm [170;175) có và nhóm 2 là nhóm [165;170) có .
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng .
Xét nhóm 4 là nhóm [175;180) có và nhóm 3 là nhóm [170;175) có .
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Khi đó,
Giải:
CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CHO MẪU SỐ LIỆU GHÉP NHÓM
BÀI 1. KHOẢNG BIẾN THIÊN, KHOẢNG TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM
HỆ THỐNG KIẾN THỨC
1. Khoảng biến thiên
Xét mẫu số liệu ghép cho ở Bảng 1:
| Nhóm | Tần số |
| ... | ... |
| Bảng 1 |
Gọi lần lượt là đầu mút trái của nhóm 1, đầu mút phải của nhóm .
Hiệu được gọi là khoảng biến thiên của mẫu số liệu ghép nhóm đó.
a) Định nghĩa
Ví dụ: Bảng 2 biểu diễn mẫu số liệu ghép nhóm về chiều cao của mẫu cây ở vườn cam (đơn vị: ). Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
Trong mẫu số liệu ghép nhóm đó, ta có: đầu mút trái của nhóm 1 là đầu mút phải của nhóm 5 là .
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:
Giải:
| Nhóm | ||||||
| Tần số |
Bảng 2
b) Ý nghĩa
- Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số liệu đó.
- Trong các đại lượng đo mức độ phân tán của mẫu số liệu ghép nhóm, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị là và của mẫu số liệu nên đại lượng đó dễ bị ảnh hưởng bởi các giá trị bất thường.
- Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc.
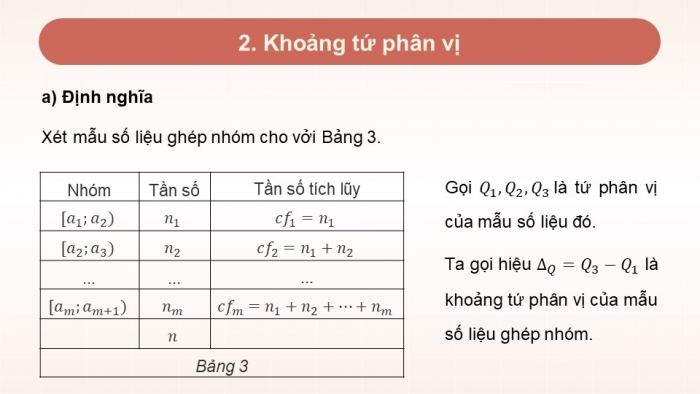
2. Khoảng tứ phân vị
Xét mẫu số liệu ghép nhóm cho vởi Bảng 3.
Gọi là tứ phân vị của mẫu số liệu đó.
Ta gọi hiệu là khoảng tứ phân vị của mẫu số liệu ghép nhóm.
a) Định nghĩa
| Nhóm | Tần số | Tần số tích lũy |
| ... | ... | ... |
| Bảng 3 |
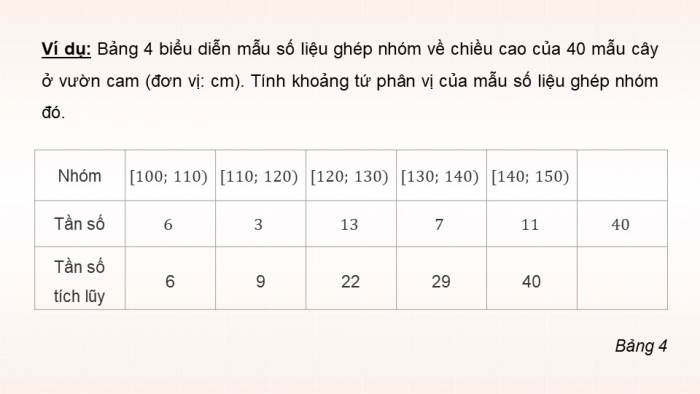
Ví dụ: Bảng 4 biểu diễn mẫu số liệu ghép nhóm về chiều cao của 40 mẫu cây ở vườn cam (đơn vị: cm). Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
| Nhóm | ||||||
| Tần số | ||||||
| Tần số tích lũy | 6 | 9 | 22 | 29 | 40 |
Bảng 4
Giải:
Số phần tử của mẫu là .
Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng .
Xét nhóm 3 là nhóm [120;130) có và nhóm 2 là nhóm [110;120) có .
Giải:
Suy ra nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng .
Xét nhóm 5 là nhóm [140;150) có và nhóm 4 là nhóm [130;140) có .
Áp dụng công thức, ta có tứ phân vị thứ ba là:
Khi đó, (cm)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là
b) Ý nghĩa
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị bất thường của mẫu đó. Khoảng tứ phân vị được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mẫu số liệu và nó không bị ảnh hưởng bởi các giá trị bất thường đó.
LUYỆN TẬP
PHIẾU BÀI TẬP SỐ 1
DẠNG 1: Xác định khoảng biến thiên của mẫu số liệu ghép nhóm
Phương pháp giải:
- Xác định là đầu mút trái của nhóm 1 (nhóm đầu tiên trong bảng).
- Xác định là đầu mút phải của nhóm (nhóm cuối cùng trong bảng).
- Tính khoảng biến thiên: .
Bài 1. Thống kê số ngày trong tháng 4 năm 2023 và năm 2024 về nhiệt độ cao nhất trong ngày tại Hà Nội, người ta thu được bảng sau:
| Nhiệt độ | [23; 26) | [26; 29) | [29; 32) | [32; 35) | [35; 38) | [38; 41) |
| Số ngày trong 4/2023 | 3 | 11 | 9 | 7 | 0 | 0 |
| Số ngày trong 4/2024 | 2 | 3 | 5 | 9 | 8 | 3 |
(Theo accuweather.com)
a) Hãy xác định khoảng biến thiên của mẫu số liệu ghép nhóm được xác định trong tháng 4/2023.
b) Hãy xác định khoảng biến thiên của mẫu số liệu ghép nhóm được xác định trong tháng 4/2024.
c) Tháng 4 năm nào ở Hà Nội nhiệt độ cao nhất trong ngày biến đổi nhiều hơn?
Giải:
a) Trong mẫu số liệu ghép nhóm, ta có:
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 4 là
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 6 là
Bài 2. Lớp 12B thi tâng cầu để lấy điểm cuối học kì I. Kết quả của 50 học sinh được cho trong bảng sau:
| Số quả | [0; 10) | [10; 20) | [20; 30) | [30; 40) | [40; 50) |
| Số học sinh | 2 | 5 | 16 | 20 | 7 |
Hãy xác định khoảng biến thiên của mẫu số liệu ghép nhóm trên.
Giải:
Trong mẫu số liệu ghép nhóm, ta có:
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 5 là
Bài 3. Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
| Thu nhập | [5; 8) | [8; 11) | [11; 14) | [14; 17) | [17; 20) |
| Số người của nhà máy A | 15 | 33 | 25 | 16 | 11 |
| Số người của nhà máy B | 22 | 20 | 31 | 20 | 0 |
a) Hãy xác định khoảng biến thiên được của mẫu số liệu ghép nhóm ở nhà máy A.
b) Hãy xác định khoảng biến thiên được của mẫu số liệu ghép nhóm ở nhà máy B.
Giải:
a) Trong mẫu số liệu ghép nhóm của nhà máy A, ta có:
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 5 là
Bài 3. Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
| Thu nhập | [5; 8) | [8; 11) | [11; 14) | [14; 17) | [17; 20) |
| Số người của nhà máy A | 15 | 33 | 25 | 16 | 11 |
| Số người của nhà máy B | 22 | 20 | 31 | 20 | 0 |
a) Hãy xác định khoảng biến thiên được của mẫu số liệu ghép nhóm ở nhà máy A.
b) Hãy xác định khoảng biến thiên được của mẫu số liệu ghép nhóm ở nhà máy B.
Giải:
b) Trong mẫu số liệu ghép nhóm của nhà máy B, ta có:
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 4 là
Bài 4: Bảng tần số ghép nhóm dưới đây thống kê theo độ tuổi số lượng thành viên nam và thành viên nữ đang sống tại một khu dân cư.
| Khoảng tuổi | [50;55) | [55;60) | [60;65) | [65;70) | [70;75) | [75;80) | [80;85) | [85;90) |
| Số thành viên nam | 6 | 5 | 4 | 10 | 9 | 4 | 2 | 0 |
| Số thành viên nữ | 3 | 5 | 7 | 7 | 8 | 4 | 4 | 2 |
a) Hãy tính các khoảng biến thiên của tuổi nam giới và nữ giới ở bảng số liệu ghép nhóm trên.
b) Hãy cho biết trong khu dân cư trên, nam giới hay nữ giới có độ tuổi phân tán hơn.
Giải:
a) Trong mẫu số liệu ghép nhóm của nam giới, ta có:
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 7 là
- Đầu mút trái của nhóm 1 là
- Đầu mút phải của nhóm 8 là
--------------- Còn tiếp ---------------
=> Xem toàn bộ Giáo án Powerpoint dạy thêm Toán 12 Cánh diều
Powerpoint dạy thêm Toán 12 CD, giáo án điện tử dạy thêm Bài 1: Khoảng biến thiên, khoáng tứ phân Toán 12 cánh diều, giáo án PPT dạy thêm Toán 12 cánh diều Bài 1: Khoảng biến thiên, khoáng tứ phân
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
