Hình II.4 vẽ quỹ đạo của một quả cầu lông được đánh lên với vận tốc ban đầu
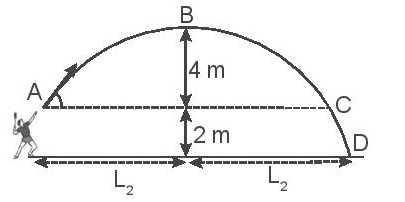
II.8 Hình II.4 vẽ quỹ đạo của một quả cầu lông được đánh lên với vận tốc ban đầu v$_{o}$ = 10 m/s ở độ cao 2 m so với mặt đất. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s$^{2}$

a) Xác định độ lớn của góc $\alpha $.
b) Xác định vận tốc của quả cầu ở vị trí B.
c) Tính khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của người đánh cầu.
a) Khi đạt độ cao cực đại thì $v_{yB}$ = 0.
$v_{yB}^{2}-v_{oy}^{2}=2gh_{1}\Rightarrow v_{o}^{2}.sin^{2}\alpha =2gh_{1}$
$\Rightarrow sin\alpha =\sqrt{\frac{2.9,8.4}{10^{2}}}=0,885\Rightarrow \alpha =62^{o}$
b) Vận tốc của cầu ở điểm B: $\vec{v_{B}}=\vec{v_{xB}}+\vec{v_{yB}}$
$\Rightarrow v_{B}=v_{o}cos\alpha +0=10.cos62^{o}\approx 4,7m/s$
c) Tầm xa: $L=L_{1}+L_{2}=v_{x}t_{1}+v_{x}t_{2}=v_{x}(t_{1}-t_{2})$
Thời gian t$_{1}$ bằng thời gian để quả cầu chuyển động từ A tới B bằng thời gian để quả cầu rơi từ độ cao B tới độ cao A. Do đó:
$t_{1}=\sqrt{\frac{2h_{1}}{g}}=\sqrt{\frac{2.4}{9,8}}=0,9s$
Thời gian t$_{2}$ bằng thời gian để quả cầu rơi từ độ cao B tới mặt đất:
$t_{2}=\sqrt{\frac{2h_{2}}{g}}=\sqrt{\frac{2.(4+2)}{9,8}}=1,1s$
Do đó: L = 4,7.(0,9 + 1,1) = 9,4 m.
Xem toàn bộ: Giải SBT Vật lí 10 Kết nối Bài tập cuối chương II

Bình luận