Giải câu 3 trang 85 toán VNEN 9 tập 1
Câu 3: Trang 85 sách VNEN 9 tập 1
Chọn đáp án đúng trong các câu sau
a) Cho $0^{\circ}$ < $\alpha $ < $90^{\circ}$. Khẳng định nào sau đây là đúng?
A. sin$\alpha $ + cos$\alpha $ = 1 B. tan$\alpha $ = tan ($90^{\circ}$ - $\alpha $)
C. sin$\alpha $ = cos($90^{\circ}$ - $\alpha $) D. cot$\alpha $ = cot($90^{\circ}$ -$\alpha $)
b) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm, BC = 7,5cm. Độ dài CH bằng:
A. 4,8cm B. 2,7cm C. 0,6cm D. $\frac{5}{3}$cm.
c) Cho tam giác ABC vuông tại A, $\widehat{B}$ = $\alpha $, AB =1cm, AC = 2cm. Khẳng định nào sau đây là sai?
A. sin$\alpha $ = 2cos$\alpha $ B.cot$\alpha $ = $\frac{1}{2}$
C. $\frac{sin\alpha - cos\alpha}{sin\alpha + cos\alpha}$ = $\frac{1}{3}$ D. $\frac{sin\alpha - 2cos\alpha}{sin\alpha + cos\alpha}$ = $\frac{1}{3}$.
a) Ta có: góc $\alpha $ và $90^{\circ}$ - $\alpha $ là hai góc phụ nhau nên: sin$\alpha $ = cos($90^{\circ}$ - $\alpha $)
Suy ra đáp án đúng là C.
b)

Ta có: AC = $\sqrt{BC^{2} + AB^{2}}$ = $\sqrt{7,5^{2} - 6^{2}}$ = 4,5cm
$AC^{2}$ = CH.BC $\Rightarrow $ CH = $\frac{AC^{2}}{BC}$ = 2,7cm
Vậy đáp án B.
c)
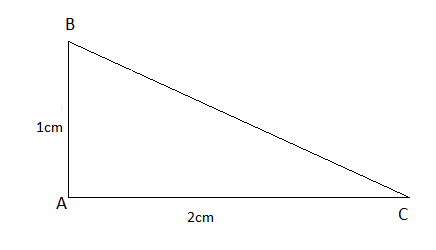
Theo định lý Py-ta-go: BC = $\sqrt{AB^{2} + AC^{2}}$ = $\sqrt{1^{2} + 2^{2}}$ = $\sqrt{5}$
*Ta có: cot$\alpha $ = $\frac{AB}{AC}$ = $\frac{1}{2}$ suy ra B đúng
* Ta có: sin$\alpha $ = $\frac{AC}{BC}$ = $\frac{2}{\sqrt{5}}$
cos$\alpha $ = $\frac{AB}{BC}$ = $\frac{1}{\sqrt{5}}$
$\Rightarrow $ sin$\alpha $ = 2cos$\alpha $ (1)
Suy ra đáp án A đúng
* Từ (1) suy ra sin$\alpha $ - 2cos$\alpha $ = 0
$\Rightarrow $ $\frac{sin\alpha - 2cos\alpha}{sin\alpha + cos\alpha}$ = 0
Suy ra đáp án D sai.
Vậy D sai.
Xem toàn bộ: Giải toán VNEN 9 bài 8: Ôn tập chương I
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận