Giải câu 11 bài: Ôn tập chương I: Khối đa diện

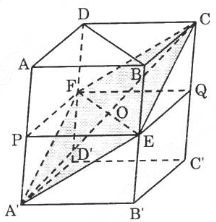Mặt phẳng (CEF) chứa đường thẳng EF mà E là trung điểm của BB', F là trung điểm của CC' nên EF chứa giao điểm O của các đường chéo của hình hộp, do đo mặt phẳng (CEF) cùng chứa giao điểm O của các đường chéo và nó cũng chứa đường chéo A'C của hình hộp. Ta dễ dàng nhận thấy rằng thiết diện chính là hình bình hành CEA'F.

Qua EF ta dựng một mặt phẳng song song với đáy của hình hộp, mặt phẳng này cắt AA' tại P và cắt CC' tại Q.

Ta có thể tích của hình hộp ABCD. PEQF là $V_{ABCD.PEQF}=\frac{1}{2} V_{ABCD.A'B'C'D'}$ (1)

Mặt khác ta có $V_{CFQE}=V_{A'FPE}$  (2) (có chiều cao và diện tích đáy bằng nhau)

Xét khối đa diện ABCDEF do mặt phẳng (CEF) chia ra trên hình hộp ABCD.A'B'C'D'có 

$V_{ABCD.FA'EQ}=V_{ABCD.FPE}+V_{A'FPE}$ (3)

Từ (1), (2), (3) suy ra $V_{ABCD.FA'EQ}=\frac{1}{2}V_{ABCD.A'B'C'D'}$.

Vậy mặt phẳng (CEF) chia hình hộp thành hai khối đa diện có thể tích bằng nhau và tỉ số của chúng là 1.