Giải câu 10 bài 2: Đường kính và dây của đường tròn sgk Toán Hình 9 tập 1 Trang 104

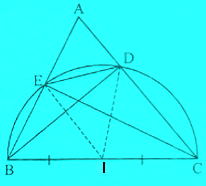
a.  Gọi I là trung điểm của BC.

Theo tính chất trung tuyến ứng với cạnh huyền ta có: 

$\left\{\begin{matrix}IE=\frac{1}{2}BC& \\ ID=\frac{1}{2}BC  & \end{matrix}\right.=> IE=ID=IB=IC=\frac{1}{2}BC$

=>   4 điểm B, C, D, E cùng thuộc đường tròn (I) đường kính BC.  ( đpcm )

b.  Ta có :  BC là đường kính của đường tròn tâm I .

Mà DE là 1 dây không qua tâm đường tròn .

=>  DE < BC .   ( đpcm )