Bài tập xác định f, d, d'
Bài 3: Một vật AB cao 1cm đặt trước một thấu kính hội tụ, ta thu được một ảnh cao 4cm như hình vẽ. Biết khoảng cách từ vật đến ảnh bằng 20cm.
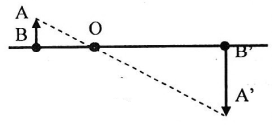
a, Xác định tính chất của ảnh.
b, Tính khoảng cách từ vật và từ ảnh đến thấu kính.
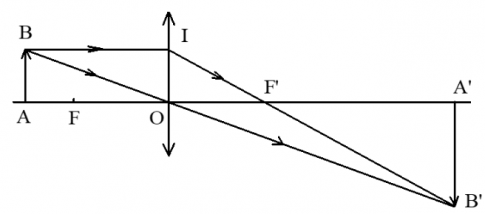
Bài 4: Cho thấu kính có tiêu cự 20 cm, vật AB đặt cách thấu kính 60 cm và có chiều cao h = 2 cm.
a, Vẽ ảnh của vật qua thấu kính.
b) Vận dụng kiến thức hình học hãy tính khoảng cách từ ảnh đến thấu kính.
Bài 5: Một vật sáng AB dạng đoạn thẳng được đặt tại một vị trí trước một thấu kính hội tụ, sao cho AB vuông góc với trục chính của thấu kính và A nằm trên trục chính. Qua thấu kính ta thu được một ảnh thật lớn gấp 2 lần vật. Sau đó, giữ nguyên vị trí vật AB và dịch chuyển thấu kính dọc theo trục chính, theo chiều ra xa vật một đoạn 10cm, thì thấy ảnh của nó cũng dịch chuyển đi một đoạn 10cm so với vị trí ảnh ban đầu. Tính tiêu cự f của thấu kính.
Bài 3:
a, Ta có sơ đồ tạo ảnh:
![]()
AB là vật thật, ảnh A'B' ngược chiều AB => A'B' là ảnh thật
b, Ta có:
Khoảng cách vật đến ảnh bằng:
BB" = BO + B'O = 20 cm(1)
Mặt khác:
$\frac{OB}{OB'}=\frac{AB}{A'B'}=\frac{1}{4}$
=> B'O = 4BO (2)
Từ (1) và (2) => BO = 4cm
Khoảng cách từ ảnh đến thấu kính bằng:
B'O = 16cm
Bài 4:
a, Vẽ ảnh:

b, Gọi Oa = d; OA' = d'; OF = OF' = f
Ta có $\Delta AOB\sim \Delta A'OB'$ nên:
$\frac{A'B'}{AB}=\frac{OA'}{OA}$ (1)
Ta có $\Delta IOF'\sim \Delta B'A'F'$ nên:
$\frac{A'B'}{OI}=\frac{A'B'}{AB}=\frac{F'A'}{F'O}$ (2)
Từ (1) và (2) => $\frac{OA'}{OA}=\frac{F'A'}{F'O}$ hay $\frac{d'}{d}=\frac{d'-f}{f}$
=> f.d' = d.d' - f.d
Chia cả hai vế cho d.d'.f => $\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}$
=> d' = $\frac{d.f}{d-f}$
Với f = 20cm; d = 60cm => d' = 30cm
Bài 5: Gọi ảnh của AB qua thấu kính lúc ban đầu là A’B’. Ảnh của AB qua thấu kính lúc sau là A’’B’’.
- Gọi khoảng cách từ vật đến thấu kính lúc đầu và lúc sau là d và d1, khoảng cách từ ảnh đến thấu kính lúc đầu và lúc sau là d’ và d’1.
Ban đầu vật cho ảnh thật nên d > f. Mà d1 = d + 10 suy ra d1 > f. Hay ảnh A’’B’’ cũng là ảnh thật.
Áp dụng công thức thấu kính hội tụ với ảnh thật ta có:
$\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}$ (*)
Ban đầu ảnh cao gấp 2 lần vật => $\frac{A'B'}{AB}=\frac{d'}{d}$ = 2
=> d' = 2d
Ta có: $\frac{1}{f}=\frac{1}{d}+\frac{1}{2d}=\frac{3}{2d}$ (1)
- Sau khi dịch thấu kính 10cm thì: d1 = d + 10.
Giả sử ảnh A''B'' di chuyển ra xa thấu kính 10cm => d’1 = d’
Thay vào (*) => $\frac{1}{f}=\frac{1}{d_{1}}+\frac{1}{d'_{1}}=\frac{1}{d+10}+\frac{1}{d'}$ (**)
(*) và (**) mâu thuẫn nhau
Vậy ảnh A’’B’’ dịch chuyển lại gần thấu kính hơn
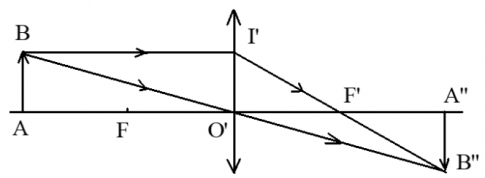
O’A” = OA’ - 10 - 10 = OA’ - 20 hay d1' = d' - 20 = 2d -20
Ta có phương trình: $\frac{1}{f}=\frac{1}{d_{1}}+\frac{1}{d'_{1}}=\frac{1}{d+10}+\frac{1}{2d-20}$ (2)
Từ (1) và (2) => $\frac{1}{f}=\frac{3}{2d}=\frac{1}{d+10}+\frac{1}{2d-20}$
=> $\frac{3}{2d}=\frac{3d-10}{2(d+10)(d-10)}$
=> 3d2 - 300 = 3d2 - 10d
=> d = 30
Thay vào (1) => $\frac{1}{f}=\frac{3}{2d}=\frac{1}{20}$
=> f = 20cm
Vậy tiêu cự thấu kính là 20cm.
Giải những bài tập khác
Giải bài tập những môn khác
Đang cập nhật dữ liệu...

Bình luận