Câu hỏi tự luận mức độ vận dụng Toán 5 ctst bài 70: Xăng-ti-mét khối
3. VẬN DỤNG (3 câu)
Câu 1: Viết số đo thể tích khối hình màu vàng dưới dạng phân số và số thập phân.

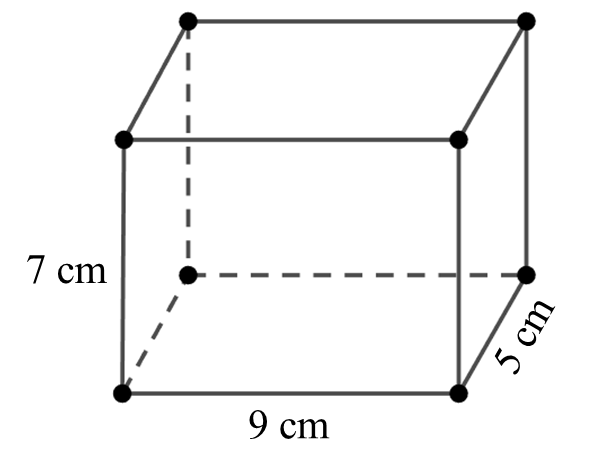
Câu 2: Một chiếc thùng có dạng hình hộp chữ nhật với các kích thước như hình dưới. Theo em, làm thế nào để biết thể tích của thùng và thể tích của thùng là bao nhiêu xăng-ti-mét khối?
Câu 3: Bạn Minh có hai cái hộp vải hình chữ nhật có kích thước khác nhau như hình dưới. Hỏi hộp vải nào có thể tích lớn hơn?
|
|
Hộp (1) | Hộp (2) |
Câu 1:
Hình lập phương to là hình lập phương có cạnh 1cm nên có thể tích là ![]() .
.
Một hình lập phương to gồm 8 hình lập phương nhỏ màu vàng nên thể tích một hình lập phương nhỏ màu vàng bằng ![]() thể tích một hình lập phương to.
thể tích một hình lập phương to.
Do đó thể tích một hình lập phương nhỏ màu vàng là: ![]()
Khối hình màu vàng có 5 hình lập phương nhỏ màu vàng.
Thể tích khối hình màu vàng dưới dạng phân số là:
![]()
Thể tích khối hình màu vàng dưới dạng số thập phân là:
![]()
Câu 2:
Để biết thể tích của thùng thì em sẽ xếp đầy thùng bằng cách hình lập phương cạnh 1 cm.
Chiều dài của thùng là 9 cm nên chứa được 9 hình lập phương cạnh 1cm.
Chiều rộng của thùng là 5 cm nên chứa được 5 hình lập phương cạnh 1cm.
Suy ra mặt đáy của thùng chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Chiều cao của thùng là 7 cm nên chứa được 7 hình lập phương cạnh 1cm.
Vậy thùng có thể chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Do đó thể tích của thùng là ![]() .
.
Câu 3:
* Hộp (1):
Chiều dài của hộp là 12 cm nên chứa được 12 hình lập phương cạnh 1cm.
Chiều rộng của hộp là 6 cm nên chứa được 6 hình lập phương cạnh 1cm.
Suy ra mặt đáy của hộp chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Chiều cao của hộp là 20 cm nên chứa được 20 hình lập phương cạnh 1cm.
Vậy chiếc hộp có thể chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Do đó thể tích của hộp (1) là ![]() .
.
* Hộp (2):
Chiều dài của hộp là 13 cm nên chứa được 13 hình lập phương cạnh 1cm.
Chiều rộng của hộp là 7 cm nên chứa được 7 hình lập phương cạnh 1cm.
Suy ra mặt đáy của hộp chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Chiều cao của hộp là 17 cm nên chứa được 17 hình lập phương cạnh 1cm.
Vậy chiếc hộp có thể chứa được ![]() hình lập phương cạnh 1cm.
hình lập phương cạnh 1cm.
Do đó thể tích của hộp (2) là ![]() .
.
Ta có: ![]() nên hộp vải (2) có thể tích lớn hơn.
nên hộp vải (2) có thể tích lớn hơn.



Bình luận