Câu hỏi tự luận mức độ vận dụng Toán 5 ctst bài 43: Hình tam giác
3. VẬN DỤNG (3 câu)
Câu 1: Quan sát các hình tam giác dưới đây và phân loại chúng theo đặc điểm độ dài các cạnh:
a. Tam giác ABC có AB = 5 cm, AC=5 cm, BC=6 cm
b. Tam giác DEF có DE=8 cm, DF=6 cm, EF=8 cm.
c. Tam giác XYZ có XY=4 cm, YZ=4 cm, XZ=4 cm.
Hỏi mỗi tam giác trên là loại tam giác nào (tam giác đều, tam giác cân, hay tam giác thường)?
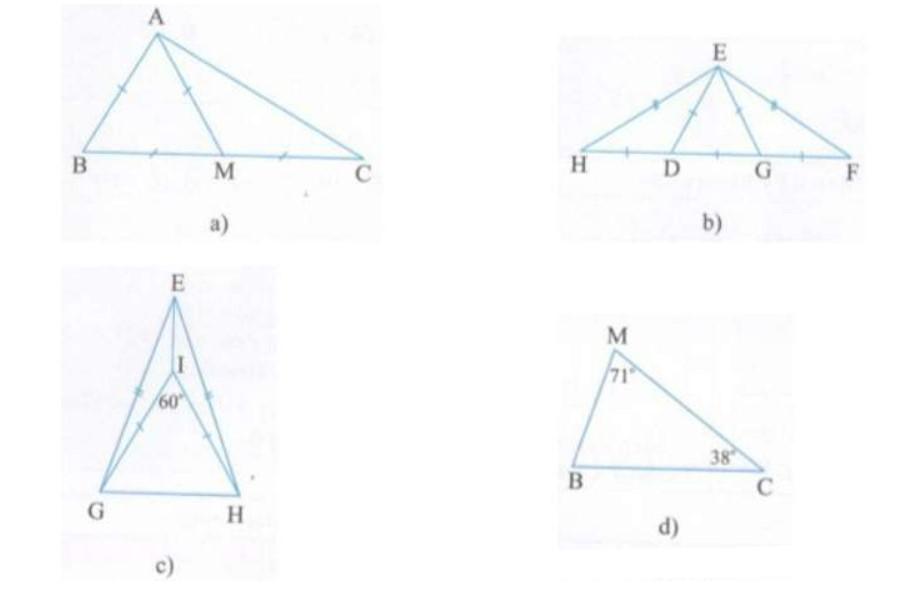
Câu 2: Trong các tam giác ở các hình a, b, c, d bên dưới, tam giác nào là tam giác cân? Tam giác nào là tam giác đều? Giải thích vì sao?
Câu 1:
a. Tam giác ABC có AB = 5 cm, AC = 5 cm, BC = 6 cm
Ta thấy AB = AC = 5 cm và BC = 6 cm.
Hai cạnh AB và AC bằng nhau, còn cạnh BC dài hơn.
Đây là một tam giác cân.
b. Tam giác DEF có DE = 8 cm, DF = 6 cm, EF = 8 cm
Ta thấy DE = EF = 8 cm và DF = 6 cm.
Hai cạnh DE và EF bằng nhau, còn cạnh DF dài hơn.
Đây là một tam giác cân.
c. Tam giác XYZ có XY = 4 cm, YZ = 4 cm, XZ = 4 cm
Ta thấy XY = YZ = XZ = 4 cm.
Tất cả ba cạnh của tam giác này đều bằng nhau.
Đây là một tam giác đều.
Câu 2:
a) Ta có: AB = BM = AM (gt) ⇒ tam giác ABM là tam giác đều.
AM = CM (gt) ⇒ tam giác MAC cân tại M.
b) Ta có: ED = DG = EG (gt) ⇒ tam giác EDG là tam giác đều.
DH = DE ⇒ tam giác DEH là tam giác cân tại đỉnh D.
Ta có: EG = GF ⇒ tam giác GEF là tam giác cân tại đỉnh G.
Ta có: EH = EF ⇒ tam giác EHF là tam giác cân tại đỉnh E.
c) Ta có: IG = IH (gt) ⇒ tam giác IGH là tam giác cân tại đỉnh I. Mà góc GIH=60 độ (gt). Do đó tam giác IGH là tam giác đều.
Ta có: EG = EH (gt) ⇒ tam giác EGH là tam giác cân tại đỉnh E.
d) Tam giác MBC có: góc M + góc B + góc C = 180 độ
Do đó: 71 độ + góc B + 38 độ = 180 độ ⇒ Góc B = 180 độ – 71 độ – 38 độ = 71 độ
Ta có: Góc B = góc M (cùng bằng 71 độ) ⇒ ΔCBM cân tại đỉnh C

Bình luận