1. BÀI TOÁN TÌM KIẾM TRÊN THỰC TẾ

Có thể nói tìm kiếm là một trong những bài toán quan trọng nhất của Tin học. Việc thiết kế thuật toán tìm kiếm sẽ phụ thuộc vào cấu trúc của miền dữ liệu cần tìm kiếm và tiêu chí cụ thể của bài toán tìm kiếm.

2. TÌM KIẾM TUẦN TỰ

• Thuật toán tìm kiếm tuần tự được thực hiện bằng cách duyệt lần lượt các phần tử của dãy từ đầu đến cuối để tìm phần tử có giá trị bằng giá trị cần tìm.
• Thuật toán tìm kiếm tuần tự có thể viết như sau:

1 deaf LinearSearch(A,K):

2    for i in range(len(A)):

3       if A[i] == K:

4           return i

5    return -1

3. TÌM KIẾM NHỊ PHÂN 

a) Phân tích bài toán

Bài toán tìm kiếm nhị phân tìm kiếm với dãy số đã được sắp xếp. Khi duyệt một phần tử bất kì của dãy số, em có thể xác định được phần tử cần tìm sẽ nằm ở bên trái hay bên phải phần tử đang duyệt, từ đó quyết định tìm tiếp theo hướng nào mà không cần duyệt tất cả các phần tử của dãy số.

b) Thuật toán tìm kiếm nhị phân

Được áp dụng cho các dãy được sắp xếp theo thứ tự xác định. Sau mỗi bước lặp của thuật toán, phạm vi tìm kiếm được thu hẹp dần. Ví dụ với dãy tăng dần, nếu giá trị cần tìm nhỏ hơn giá trị của phần tử ở giữa của dãy thì phạm vi tìm kiếm thu hẹp vào nửa đầu của dãy, ngược lại, phạm vi tìm kiếm là nửa cuối của dãy. Cứ tiếp tục như vậy cho đến khi tìm thấy hoặc phạm vi tìm kiếm bằng rỗng.

c) Minh họa các bước của thuật toán tìm kiếm nhị phân

Giả sử dãy số đã sắp xếp là A = [1, 3, 4, 7, 8, 9, 10]. Giá trị cần tìm là K = 9.

Bước 1. Phạm vi tìm kiếm là các phần tử được in đậm [1, 3, 4, 7, 8, 9, 10]

1 left = 0, right = 6

2 mid = (0 + 6) // 2 = 3

3 A[mid] = A[3] = 7 < K # phần tử cần tìm nằm ở dãy con bên phải

Cập nhật chỉ số left = mid + 1 = 3 + 1 = 4

Bước 2. Phạm vi tìm kiếm là các phần tử được in đậm [1, 3, 4, 7, 8, 9, 10]

1 left = 4, right = 6

2 mid = (4 + 6) // 2 = 5

3 A[mid] = A[5] = 9 < K # phần tử cần tìm có chỉ số 5. Kết thúc chương trình.

Sơ đồ minh họa

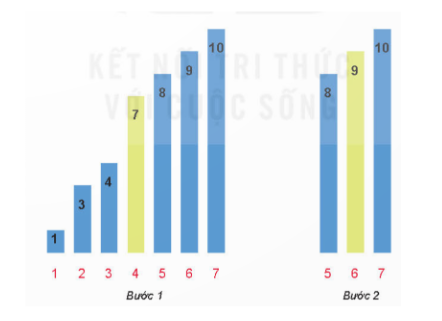
→ Thuật toán tìm kiếm nhị phân trên dãy số đã sắp xếp tăng dần có thể như sau, trong đó hàm BinarySearch(A,K) trả lại chỉ số I nếu tìm thấy A[i] = K và trả lại giá trị -1 nếu không tìm thấy K trong dãy A.

1 def BinarySearch(A,K):

2   left = 0

3   right = len(A) – 1

4   while left <= right:

5      mid = (left + right)//2

6      if A[mid] == K:

7        return mid

8      elif A[mid] < K:

9        left = mid + 1

10     else:

11       right = mid – 1

12 return -1