• Ôn tập lý thuyết
• Hướng dẫn giải bài tập sgk

A. LÝ THUYẾT

II. Định nghĩa

Định nghĩa

• Cho điểm O và số k # 0. Phép biến hình biến mỗi điểm M thành điểm M' sao cho \(\overrightarrow{OM'} = k . \overrightarrow{OM}\), được gọi là phép vị tự tâm O, tỉ số k
• Phép vị tự tâm O, tỉ số k và thường được kí hiệu là \({V_{(O,k)}}^{}\)

Nhận xét

• 1) Phép vị tự biến tâm vị tự thành chính nó
• 2) Khi k=1, phép vị tự là phép đồng nhất
• 3) Khi k = -1, phép vị tự là phép đối xứng qua tâm vị tự
• 4) $M' = V_{O,k} (M) \Leftrightarrow  M = V_{o,\frac{1}{k}}  (M')$

II. Tính chất

Tính chất 1:

• Nếu phép vị tự tâm O tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M', N' thì \(\overrightarrow{M'N'} = k. \overrightarrow{MN}\) và M'N' = |k| MN

Tính chất 2:

Phép vị tự tỉ số k :

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy

b) Biến đường thẳng thành đường thẳng song song với nó, biến tia thành tia, biến đoạn thẳng có độ dài bằng a thành đoạn thẳng có độ dài bằng |k| a

c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là  |K|, biến góc thành góc bằng nó

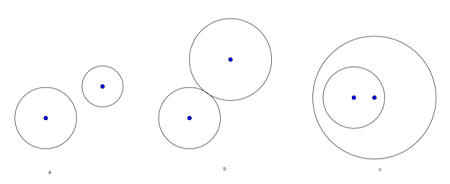
d) Biến đường trong bán kình R thành đường tròn bán kính |k|R