Giải Bài 5: Khoảng cách
Trong không gian, khoảng cách được tính như thế nào? Để biết chi tiết hơn, Tech12h xin chia sẻ với các bạn bài 5: Khoảng cách. Với kiến thức trọng tâm và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các bạn học tập tốt hơn.

A. TÓM TẮT KIẾN THỨC
1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng
Định nghĩa
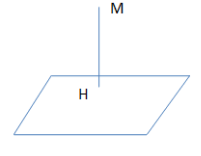
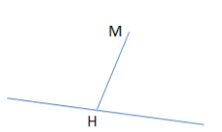
Khoảng cách từ 1 điểm M đến một mặt phẳng (P) (hoặc đến đường thẳng ∆) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P), kí hiệu là d(M, (P)) (hoặc trên đường thẳng ∆, kí hiệu là d(M, ∆) .
2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
Định nghĩa
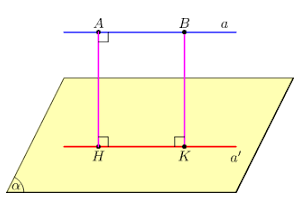
Khoảng cách giũa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì của a tới mặt phẳng (P) (h.3.57), kí hiệu là d(a, (P)).
Định nghĩa
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này tới mặt phẳng kia.
3. Khoảng cách giữa hai đường thẳng chéo nhau
Định nghĩa
- Đường thẳng c cắt và vuông góc với cả a và b gọi là đường vuông góc chung của a và b.
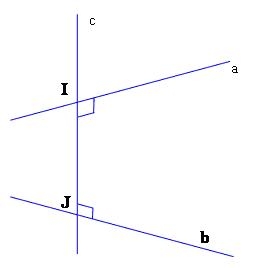

- Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng chéo nhau đó.
Nhận xét
Khoảng cách giữa hai đường thẳng chéo nhau bằng:
- Khoảng cách từ một trong hai đường thẳng đã cho đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
- Khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó (h.3.59).
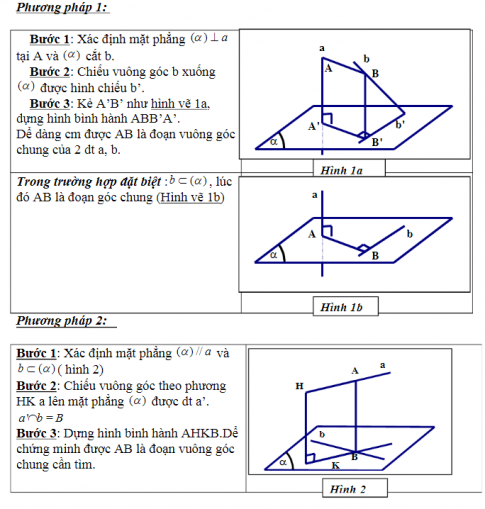
4. Cách xác định đường vuông góc chung của hai đường thẳng chéo nhau
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận