Người ta đổ thêm 100 cm3 nước vào một nhánh của một bình hình chữ U có hai nhánh giống nhau đang chứa thủy ngân

Mặt thoáng của thủy ngân ban đầu ở vị trí A. Khi đổ thêm nước vào thì A ở nhánh có nước chuyển xuống B, mặt thoáng ở nhánh còn lại chuyển tới C, như hình vẽ.

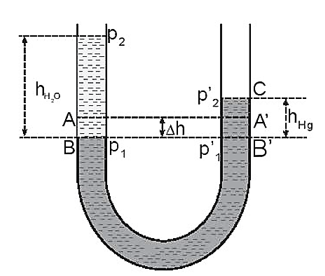
Ta có: AB = A'C => h_Hg = B'C = 2A'C; AB = $\frac{h_{Hg}}{2}$

$h_{H_{2}O}=\frac{100}{\pi R^{2}}=\frac{100}{\pi (\frac{2}{2})^{2}}$ = 31,8 cm

Gọi áp suất ở mặt thoáng của nước là p₂: p₂ = p_a (áp suất khí quyển)

Gọi áp suất ở mặt thoáng của Hg là p'₂: p'₂ = p_a, suy ra p₂ = p'₂ (1)

Gọi áp suất của nước ở B là p₁; áp suất của thủy ngân ở B' là p'₁.

Vì B và B' nằm trên cùng một mặt phẳng ngang nên p₁ = p'₁ (2)

Ta có: $\Delta p=p_{1}-p_{2}=\rho _{H_{2}O}g.h_{H_{2}O}$

$\Delta p'=p'_{1}-p'_{2}=\rho _{Hg}.g.h_{Hg}$

Từ (1) và (2) => $\Delta p=\Delta p'$

=> $\rho _{H_{2}O}g.h_{H_{2}O}=\rho _{Hg}.g.h_{Hg}$ => h_Hg = 31,8.$\frac{1000}{13600}$ = 2,34 cm.

=> $\Delta h=\frac{h_{Hg}}{2}$ = 1,17 cm.