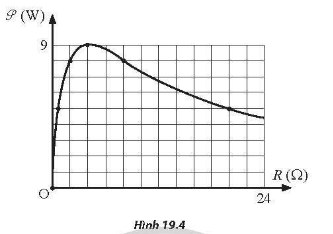
Mắc hai đầu một biến trở R vào hai cực của một nguồn điện không đổi. Điều chỉnh giá trị biến trở R. Bỏ qua điện trở của các đầy nổi. Đô thị biểu diễn sự phụ thuộc của công suất toả nhiệt trên biến trở P theo R như Hình 19,4,

01 Đề bài:

Bài 19.6 (VD): Mắc hai đầu một biến trở R vào hai cực của một nguồn điện không đổi. Điều chỉnh giá trị biến trở R. Bỏ qua điện trở của các đầy nổi. Đô thị biểu diễn sự phụ thuộc của công suất toả nhiệt trên biến trở P theo R như Hình 19,4,

a) Tính suất điện động và điện trở trong của nguồn điện.

b) Giả sử tăng R tuyển tính theo thời gian, bắt đầu từ giá trị 0 đến rất lớn. Thời điểm t= 12,5 s kể từ lúc bắt đầu tăng, công suất P đạt giá trị cực đại. Tỉnh khoảng thời gian giữa hai lần liên tiếp công suất P đạt giá trị 5 W.

02 Bài giải: