1. KHÁI NIỆM GÓC

Góc là hình gồm hai tia chung gốc.

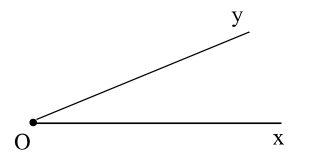
* Chú ý:

- Góc xOy (hoặc góc yOx) được kí hiệu là xOy (hoặc yOx).

- Hai tia Ox và Oy được gọi là hai cạnh của góc. Gốc chung O của hai tia được gọi là đỉnh của góc.

Luyện tập 1

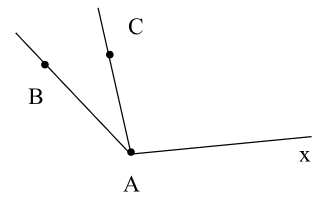
- Góc BAx có hai cạnh AB và Ax.

- Góc CAx có hai cạnh AC và Ax.

- Góc BAC có hai cạnh AB và AC.

2. ĐIỂM NẰM TRONG GÓC

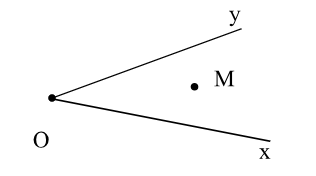
Hình 73

Điếm M như trong Hình 73 (không thuộc tia Ox, Oy) được gọi là điểm nằm trong góc xOy hay điểm trong của góc xOy.

Luyện tập 2

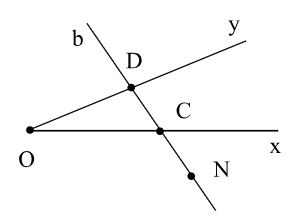
Ba điểm D, C, N thẳng hàng và điểm N không nằm giữa hai điểm D và C.

3. SỐ ĐO CỦA GÓC

3.1. Đo góc

- Thước đo góc có dạng nửa hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với 1°.

- Dùng thước đo góc để xác định số đo của góc xOy.

+ Bước 1: Đặt thước đo góc sao cho tâm của thước trùng với đỉnh của góc. Vạch 0 của thước nằm trên cạnh Ox.

+ Bước 2: Xác định xem cạnh Oy đi qua vạch chia độ nào thì đó chính là số đo của góc.

Kết luận: Mỗi góc một số đo

Chú ý:

+ Nếu số đo của góc xOy là n° thì ta kí hiệu $\widehat{xOy}$ = n°hoặc $\widehat{yOx}$ = n°

+ Trong hình 77b, số đo góc xOy là 40° nên ta viết $\widehat{xOy}$ = 40°

+ Chúng ta chỉ xét các góc có số đo không vượt quá 180°.

Luyện tập 3

Chú ý:

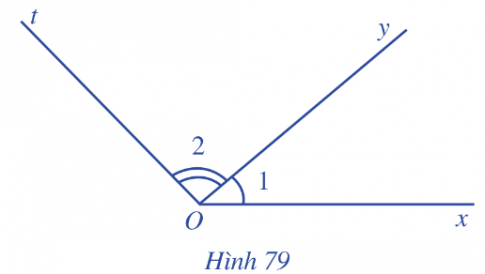
Trong một hình có nhiều góc, người ta thường vẽ thêm một hay nhiều vòng cung nhỏ nối hai cạnh của góc đó để dễ thấy góc mà ta đang xét tới. Khi cần phân biệt các góc có chung một đỉnh, chẳng hạn chung đỉnh O trong Hình 79, ta dùng kí hiệu $\widehat{O_{1}}$,  $\widehat{O_{2}}$

3.2. So sánh hai góc

Ta có thể so sánh hai góc dựa vào số đo của chúng.

+ Nếu số đo cùa góc xOy bằng số đo của góc uPv thì góc xOy bằng góc uPv và được kí hiệu là $\widehat{xOy}=\widehat{uPv}$

+ Nếu số đo của góc xOy lớn hơn số đo của góc uPv thì góc xOy lớn hơn góc uPv và được kí hiệu là $\widehat{xOy}>\widehat{uPv}$

+ Nếu số đo của góc xOy nhỏ hơn số đo của góc uPv thì góc xOy nhỏ hơn góc uPv và được kí hiệu là $\widehat{xOy}<\widehat{uPv}$

Luyện tập 4

Hình 81

a) $\widehat{ABC}=\widehat{ACB}$

b) $\widehat{ACB}=\widehat{ADB}$

4. GÓC VUÔNG, GÓC NHỌN, GÓC TÙ, GÓC BẸT

- Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°.

- Góc vuông là góc có số đo bằng 90°.

- Góc tù là góc có số đo lớn hơn 90° và nhỏ hơn 180°.

- Góc bẹt là góc có số đo bằng 180°.

- Trong Hình 82b, ta có:

+  $\widehat{xOy}$là góc nhọn;

+ $\widehat{xOz}$là góc vuông; 

+ $\widehat{xOt}$là góc tù; 

+ $\widehat{xOm}$là góc bẹt.

Luyện tập 5 

1 - c ; 2 - a ; 3 - b