Lý thuyết trọng tâm Tin học 10 cánh diều bài 17: Thực hành lập trình giải bài toán trên máy tính
Tổng hợp kiến thức trọng tâm Tin học 10 cánh diều bài 17: Thực hành lập trình giải bài toán trên máy tính. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
I. Bài 1
Nhận xét để xác định bài toán:
Vì mỗi giờ, khoảng cách giữa hai tàu giảm đi (v1 + v2) hải lí, vì vậy để hai tàu gặp nhau, sẽ cần giờ.
- Sử dụng kiến thức vật lí để giải thích:
Đặt hệ quy chiếu một chiều với điểm 0 ở vị trí tàu cá và đảo ở vị trí d.
Phương trình chuyển động của tàu cá: x = 0 + v1.t
Phương trình chuyển động của tàu cứu hộ: x = d – v2.t
Yêu cầu tìm t để 0 + v1.t = d – v2.t, tức là tìm t = ,có thể giải bằng thuật toán giải phương trình bậc nhất.
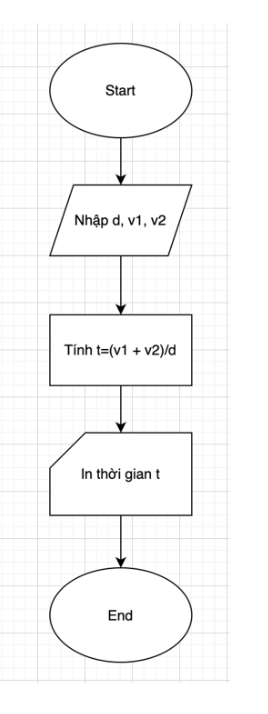
Thuật toán:
Bước 1: Nhập vào d, v1, v2.
Bước 2: Tính t = d/(v1+v2).
Bước 3: In ra t.
Chương trình:

Kiểm thử: Đề xuất các bộ test và thực hiện kiểm thử.
II. Bài 2
Xác định bài toán:
Input: Các dữ liệu
- Số liều đã có m ( ).
- Số liều cần có n ( ).
- Năng suất một ngày: cơ sở A sản xuất pa, cơ sở B sản xuất pb liều vacxin, ( )
Output: Số ngày để sản xất đủ vacxin: k ngày.
Thuật toán
Ta xét một thuật toán đơn giản: Mô phỏng đúng quá trình sản xuất, sau mỗi ngày thì số liều đã có tăng lên (pa + pb) và lặp đi lặp lại cho tới khi đủ số liều cần có.
Bước 1: Nhập vào n, m, pa, pb.
Bước 2: k = 0
Bước 3: while m < n: # chừng nào chưa đủ số liều
Bước 4: k +=1# thêm một ngày.
Bước 5: m + = pa + pb # số liều được thêm pa + pb sau một ngày.
Bước 6: In ra k # in ra số ngày.
Chương trình 1:

Kiểm thử
Xây dựng bộ test:
Dữ liệu | Kết quả thực hiện | Ý đồ test |
200 50 20 35 | 3 | Bộ test 1: Test ví dụ đề bài |
200 50 4 6 | 15 | Bộ test 2: Sản xuất thêm 15 ngày, không thừa liều nào |
201 50 4 6 | 16 | Bộ test 3: Sản xuất thêm 16 ngày, thừa ra 9 liều |
1000 1000 1 2 | 0 | Bộ test 4: Số liều đã đủ, không cần sản xuất thêm |
100000000 0 1 1 | 50 000 000 | Bộ test 5: Cần sản xuất thêm rất nhiều ngày |
12 16 1 2 | 0 | Bộ test 6: Số liều đã thừa, không cần sản xuất thêm |
12 16 0 0 | 0 | Bộ test 7: Không cần sản xuất thêm, pa = pb = 0 |
16 12 0 0 | -1 | Bộ test 8: không thể sản xuất đủ |
100000000 0 100000 100000 | 500 | Bộ test 9: Dữ liệu max |
Kết quả thực hiện:
Test | Kết quả mong muốn | Kết quả thực hiện | Tình trạng |
1 | 3 | 3 | OK |
2 | 15 | 15 | OK |
3 | 16 | 16 | OK |
4 | 0 | 0 | OK |
5 | 50000000 | 50000000 | Chạy rất chậm |
6 | 0 | 0 | OK |
7 | 0 | 0 | OK |
8 | -1 |
| Lặp vô hạn |
9 | 500 | 500 | OK |
Có 2/9 bộ test chương trình không đạt yêu cầu, cần hiệu chỉnh thuật toán và chương trình để khắc phục các lỗi này. Ở bộ test số 5, chương trình chạy chậm do vòng lặp while () phải thực hiện tới 50 triệu lần. Trước hết ta thử tối ưu chương trình:
Thay vì duy trì số liều đã có m và số liệu cần có n. Ta tính trước số liệu còn thiếu q = n - m.
Thay vì phải tính số liệu sản xuất ra trong một ngày bằng (pa + pb), ta tính trước luôn p = pa + pb.
Chương trình 2:

Chương trình vẫn chưa có cải thiện đáng kể về tốc độ, cụ thể là test số 5 vẫn rất chậm. Việc điều chỉnh cần được thực hiện ở mức thuật toán.
Có thể thấy rằng để sản xuất q liều với tốc độ p liều một ngày thì cần ngày. Vì vậy để tính số ngày k, ta không cần dùng vòng lặp mà có thể tính:
k = math.ceil(q/p)
Hoặc dùng công thức sau để tránh phép chia số thực:
k= (q + p -1)//p
Chương trình 3:

Kết quả thực hiện:
Test | Kết quả mong muốn | Kết quả thực hiện | Tình trạng |
1 | 3 | 3 | OK |
2 | 15 | 15 | OK |
3 | 16 | 16 | OK |
4 | 0 | 0 | OK |
5 | 50000000 | 50000000 | Chạy rất chậm |
6 | 0 | -1 | Sai |
7 | 0 |
| Chạy sinh lỗi |
8 | -1 |
| Chạy sinh lỗi |
9 | 500 | 500 | OK |
Chúng ta vừa xử lí được bộ test số 5 thì lại phát sinh lỗi ở bộ test số 6, 7. Bộ test số 8 tuy không còn rơi vào vòng lặp vô hạn nhưng lại phát sinh lỗi. Vấn đề được xác định nằm trong lập luận: "để sản xuất q liều với tốc độ p liều một ngày thì cần![]() ngày ". Với ràng buộc dữ liệu của đề bài, có thể xảy ra trường hợp q < 0 hoặc p = 0. Vi vậy ta cần phải xử lí riêng những trường hợp đó bằng cách thêm if:
ngày ". Với ràng buộc dữ liệu của đề bài, có thể xảy ra trường hợp q < 0 hoặc p = 0. Vi vậy ta cần phải xử lí riêng những trường hợp đó bằng cách thêm if:
- Nếu , tức là số vacxin đang có đã đủ, đáp số k = 0 ngày.
- Nếu q > 0:
+ Nếu p = 0, tức là không bao giờ có thể sản xuất đủ số vacxin, ta đưa ra output k = -1.
+ Nếu p > 0, đáp số ![]()
Chương trình 4:

Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận