BÀI 1. DAO ĐỘNG ĐIỀU HÒA

KHỞI ĐỘNG 

Câu hỏi: Hằng ngày, chúng ta thấy rất nhiều chuyển động, trong đó, có những vật chuyển động qua lại quanh một vị trí cân bằng. Chuyển động của người chơi đu là một ví dụ như vậy (Hình 1.1). Những chuyển động đó được gọi là dao động. Mô tả dao động như thế nào?

Giải nhanh:

Chuyển động của người chơi đu là một dạng dao động lặp lại, có tính chất chu kỳ. Khi người chơi đu thả xuống, trọng lực sẽ tác động lên cơ thể và kéo người chơi xuống dưới. Khi người chơi đạt đến điểm ngang mặt đất trong dao động, tốc độ sẽ đạt đến giá trị lớn nhất và năng lượng cơ học sẽ được chuyển đổi thành năng lượng động học.

I. DAO ĐỘNG

1. Thí nghiệm tạo dao động

Câu hỏi 1: Dùng một lò xo, một quả cầu nhỏ bằng kim loại, sợi dây và giá thí nghiệm, thảo luận với bạn xây dựng phương án và thực hiện phương án tạo ra dao động của quả cầu treo ở một đầu lò xo.

Giải nhanh:

Dụng cụ: một lò xo, một quả cầu nhỏ bằng kim loại, sợi dây và giá thí nghiệm

Tiến hành:

Bước 1: Gắn quả cầu vào sợi dây
Bước 2: Treo lò xo và quả cầu lên giá thí nghiệm
Bước 3: Kéo quả cầu lên và thả nó
Bước 4: Quan sát và đo chu kỳ dao động

Câu hỏi 2: Nêu ví dụ về dao động mà bạn quan sát được trong thực tế.

Giải nhanh:

• Quả lắc đồng hồ
• Dao động tay khi đánh bóng, đánh cầu
• Dao động của dây đàn

2. Dao dộng tự do

 Câu hỏi 3: Với một cái thước mỏng đàn hồi, hãy đề xuất phương án tạo ra dao động tự do của thước và mô tả cách làm.

Giải nhanh:

Dụng cụ : Thước mỏng, một vật nặng 

Mô tả: Khi móc vật nặng lên đầu thước, cần đảm bảo rằng vật nặng không quá nặng, không gây biến dạng quá lớn cho thước và cũng không quá nhẹ, không đủ để tạo ra dao động. Khi thả thước và vật nặng, ta cần đảm bảo rằng thước không bị gập hoặc chạm vào bất kỳ vật nào khác, để đảm bảo dao động tự do của thước. Ngoài ra, ta cũng nên lặp lại quá trình này nhiều lần để có được kết quả chính xác nhất.

Luyện tập 1: Nếu bỏ qua lực cản, chuyển động nào sau đây là dao động tự do?

A. Một con muỗi đang đập cánh.

B. Tòa nhà rung chuyển trong trận động đất.

C. Mặt trống rung động sau khi gỗ.

D. Bông hoa rung rinh trong gió nhẹ.

Giải nhanh:

C. Mặt trống rung động sau khi gỗ.

3. Biên độ, chu kì, tần số của dao 

Câu hỏi 4: Từ đồ thị Hình 1.7, mô tả sự thay đổi li độ của xe theo thời gian.

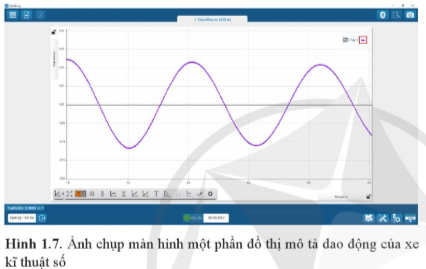
Giải nhanh:

Đồ thị là đồ thị hàm sin. Vật bắt đầu chuyển động tại vị trí có li độ lớn nhất, sau đó li độ giảm dần đến 0 rồi đến li độ nhỏ nhất. Li độ từ giá trị nhỏ nhất lại tăng dần đến 0 rồi đến giá trị lớn nhất. Sau đó, quá trình lặp lại, 

Câu hỏi 5: Tìm mối liên hệ giữa chu kì T và tần số f của dao động.

Giải nhanh:

Mối liên hệ giữa chu kì T và tần số f của dao động: 

Luyện tập 2: Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ – thời gian được biểu diễn ở Hình 1.9.

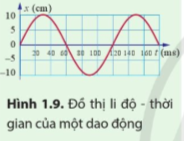
Giải nhanh:

Biên độ: A = 10 cm 

Chu kì: T = 120 s

Tần số: 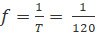(Hz)

Vận dụng: Tim co bóp theo nhịp do được điều khiển bằng một hệ thống các xung điện dẫn truyền trong cơ tim. Máy điện tim ghi nhận những xung điện này và hiển thị dưới dạng đường điện tâm đồ. Đó là những đường gấp khúc, lên xuống biến thiên theo nhịp co bóp của tim.

Dựa vào hình ảnh điện tâm đồ ở Hình 1.10, xác định chu kì đập của tim. Biết rằng mỗi khoảng vuông (theo chiều ngang) tương ứng với khoảng thời gian 0,12 s.

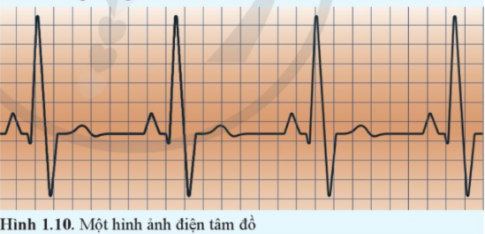
Giải nhanh:

Xác định chu kì T dựa vào việc tính độ dài từ A đến B.

Từ A đến B có xấp xỉ 7,5 ô vuông.

Suy ra chu kì T = 7,5.0,12 = 0,9 s

II. DAO ĐỘNG ĐIỀU HÒA 

1. Định nghĩa 

Câu hỏi 6: Thế nào là dao động điều hoà?

Giải nhanh:

Dao động điều hoà là dao động trong đó li độ của vật là một hàm côsin (hoặc sin) của thời gian.

Dao động điều hoà cũng có các đại lượng biên độ A, chu kì T, tần số f như đã được định nghĩa ở phần trước.

2. Tần số góc

Câu hỏi 7: Tần số góc và tần số của dao động điều hoà có liên hệ như thế nào?

Giải nhanh:

Mối liên hệ giữa tần số, chu kì, tần số góc trong dao động điều hòa:

3. Vận tốc và gia tốc trong dao động điều hòa 

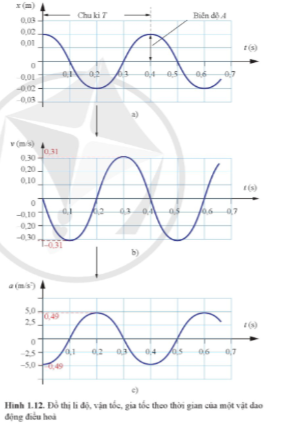
Câu hỏi 8: Dựa vào đồ thị Hình 1.12, xác định các đại lượng sau:
a) Tần số góc của dao động.

b) Biên độ của dao động.

c) Vận tốc cực đại của vật dao động.

d) Gia tốc cực đại của vật dao động.

Giải nhanh:

a) Từ đồ thị hình 1.12a ta xác định được chu kì T = 0,4 s

Tần số góc:  

b) Biên độ: A = 0,02 m = 2 cm

c) Từ đồ thị hình 1.12b ta xác định được vận tốc cực đại: v_max = 0,3 m/s

d) Từ đồ thị hình 1.12c ta xác định được gia tốc cực đại: a_max = 5 m/s2

4. Pha của dao động và độ lệch pha 

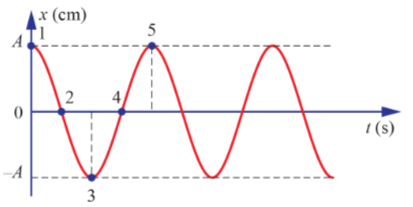
Câu hỏi 9: Xác định pha của dao động tại vị trí 3 và vị trí 4

Giải nhanh:

Li độ  x = Acos(ωt + φ)

Tại thời điểm t = 0, li độ x = A. Do đó, pha ban đầu của dao động là = 0 

Vật chuyển động trong thời gian T/2 đến vị trí 3, thực hiện nửa dao động tương ứng với góc π rad.

Pha của dao động tại vị trí 3 là 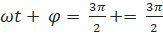(rad)

Vật chuyển động trong thời gian 34 đến vị trí 3, thực hiện 34 dao động tương ứng với góc 3π2 rad.

Pha của dao động tại vị trí 3 là 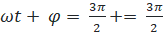(rad)

Luyện tập 3: Một vật dao động điều hòa với phương trình li độ: x = 5 cos(10 t+  (cm). Xác định pha của dao động tại thời điểm 1/30 s.

Giải nhanh:

Tính giá trị của biểu thức ωt + φ khi t = 1/30 s. Ta có:

rad

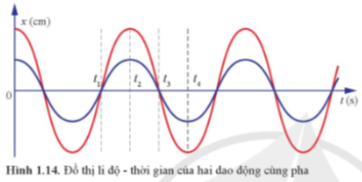
Luyện tập 4: Mô tả trạng thái của hai vật dao động ở thời điểm t₃ và t₄ trong  thị Hình 1.14.

Giải nhanh:

Tại vị trí t3 hai vật đều đang ở vị trí cân bằng và di chuyển theo chiều dương của trục toạ độ. Tại thời điểm t4 hai vật đều đang ở vị trí biên âm. 

Luyện tập 5: Đồ thị Hình 1.18 biểu diễn hai dao động ngược pha. Dựa vào đồ thị, xác định độ lệch pha của hai dao động này.

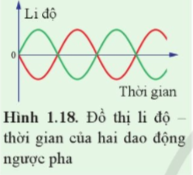
Giải nhanh:

Hai dao động cùng chu kì dao động là T

Độ lệch thời gian của hai dao động khi cùng trạng thái là

 

Độ lệch pha của hai dao động: dao động Δφ=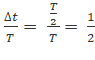 dao động

Một dao động tương ứng với  2π (rad) 

⇒ Δφ = .2π = π

Câu hỏi khám phá: 

Dụng cụ

Quả cầu kim loại nhỏ, sợi dây mảnh nhẹ, giá thí nghiệm.

Tiến hành

+ Treo quả cầu vào giá thí nghiệm.

+ Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng, kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay cho quả cầu chuyển động (Hình 1.2).

+ Mô tả chuyển động của quả cầu.

Giải nhanh:

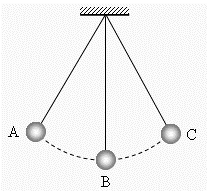
Quả cầu sẽ chuyển động từ vị trí bắt đầu được thả  biên A về vị trí cân bằng ở B và chuyển động đến vị trí  biên C  Sau đó từ vị trí biên C chuyển động về vị trí cân bằng B và trở về biên A. Nếu không có ma sát thì chuyển động của quả cầu diễn ra lặp lại, liên tục

Tìm hiểu thêm: Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này, có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b). Ví dụ, trong Hình 1.12a, tại t = 0, độ dốc của đồ thị li độ – thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ – thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s... Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.

Dựa vào các đồ thị ở Hình 1.12, tìm:

Các thời điểm gia tốc của xe bằng 0.

Các thời điểm gia tốc của xe cực đại.

Giải thích cách làm.

Giải nhanh:

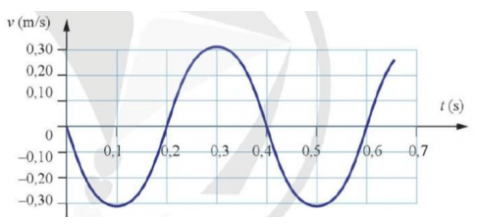
Dựa vào độ dốc của đồ thị vận tốc – thời gian ta có thể xác định được gia tốc của vật.

- Tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s gia tốc của xe bằng 0 vì độ dốc của đồ thị (v – t) tại các thời điểm đó bằng 0.

- Tại các thời điểm t = 0,2 s; 0,4 s; 0,6 s gia tốc của xe cực đại vì độ dốc của đồ thị (v – t) tại các thời điểm đó lớn nhất.