Từ thời xa xưa, Aristarchus (A – rít – ta – chớt)(310 – 230 TCN) đã biết sử dụng những thiết bị đơn giản để đo được
Bài 3. Từ thời xa xưa, Aristarchus (A – rít – ta – chớt)(310 – 230 TCN) đã biết sử dụng những thiết bị đơn giản để đo được:
a. Đường kính của Mặt Trời. Thiết bị này có cấu tạo như hình 6P.3

Em hãy thử làm thiết bị này và tiến hành đo các giá trị cần thiết. Sau đó, hãy tìm hiểu khoảng cách Trái Đất – Mặt Trời để tính ra đường kính ước lượng của Mặt Trời.
b. Khoảng cách Trái Đất – Mặt Trăng. Thiết bị này có cấu tạo như hình 6P.4
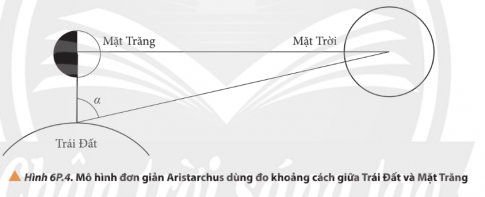
Giá trị mà Aristarchus có với góc đo là $\alpha =87^{o}$ và khoảng cách ước lượng là ES = 19 EM (ES: khoảng cách giữa Trái Đất và Mặt Trời, EM: khoảng cách giữa Trái Đất và Mặt Trăng). Ngày nay, giá trị này là $\alpha =89^{o}51'$ và ES = 400EM.
Dựa vào các giá trị trên, em hãy tính các giá trị khoảng cách giữa Trái Đất và Mặt Trăng tương ứng. So sánh kết quả tính toán được với giá trị chính xác mà em tìm được từ sách hoặc internet.
a. Áp dụng tính chất tam giác đồng dạng, ta có hệ thức tỉ lệ: $\frac{D}{d}=\frac{L}{l}$
Như vật chỉ cần đo chiều dài l của hộp quan sát, đường kính vùng sáng d của Mặt Trời trong hộp, ta có thể tính được đường kính ước lượng của Mặt Trời: $D=\frac{L.d}{l}$
b. Giá trị của Aristarchus: $\alpha =87^{o}\Rightarrow ES=\frac{EM}{cos\alpha }\approx $ 19 EM (1)
Giá trị ngày nay: $\alpha =89^{o}51'\Rightarrow ES=\frac{EM}{cos\alpha }\approx $ 382 EM (2)
So với giá trị chính xác hiện tại, ES $\approx $ 382 EM (ES = 149,6.10$^{6}$ km, EM = 384400 km) thì kết quả (2) chính xác hơn.

Bình luận