Giải câu 4 trang 43 sách toán VNEN lớp 9 tập 1
Câu 4: Trang 43 sách toán VNEN lớp 9 tập 1
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm sô:
y = $\frac{1}{2}$x + 2 và y = -x + 2
b) Gọi giao điểm của hai đường thẳng y = $\frac{1}{2}$x + 2 và y = -x + 2 với trục hoành theo thứ tự là A, B và gọi giao điểm của hay đường thẳng đó là C. Tính số đo góc A của tam giác ABC (làm tròn đến phút).
c) Tính chu vi và diện tích của tam giác ABC (đơn vị trên các trục tọa độ là xen-ti-mét )
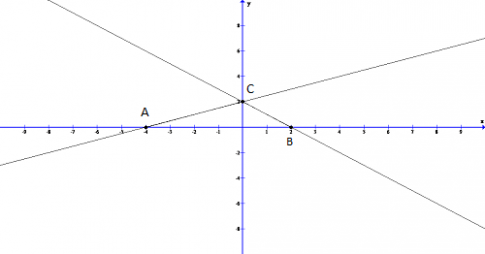
b) Gọi góc tạo bởi đường thẳng AC và trục Ox là $\alpha$, ta có $\widehat{CAB}$ = $\alpha$
Xét tam giác OAC vuông tại O, ta có: tan $\alpha$ = $\frac{OC}{OA}$ = $\frac{2}{4}$ = $\frac{1}{2}$
Suy ra $\alpha$ = 26$^{\circ}$34'
c) Ta có AC = $\sqrt[2]{OC^{2} + OA^{2}}$ = $\sqrt{4 + 16 }$ = 2$\sqrt{5}$
BC = $\sqrt{ OC^{2} + OB^{2}}$ = $\sqrt{4 + 4 }$ = 2$\sqrt{2}$
Chu vi của tam giác ABC = AB + BC + CA = 6 + 2$\sqrt{2}$ + 2$\sqrt{5}$ $\approx$ 13,3 (cm)
Diện tích tam giác ABC = $\frac{1}{2}$. OC.AB = $\frac{1}{2}$.2.6 = 6 (cm$^{2}$)
Giải những bài tập khác
Bình luận